Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 18
Resolva o problema 3.17 considerando que a direção de seja invertida.
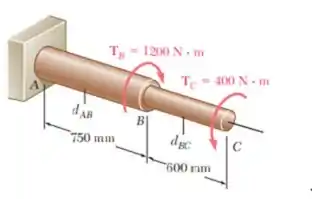
PROBLEMA 3.17 O eixo sólido mostrado é formado por um latão para cuja tensão de cisalhamento admissível é de 55 MPa. Negligencie o efeito das concentrações de tensão, determine os menores diâmetros para o qual a tensão de cisalhamento permitida não é excedida.
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente determine os menores diâmetros Observe que a direção do TC foi invertida na figura.
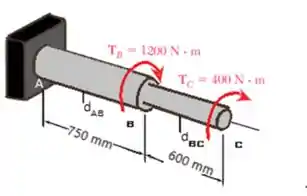
Sabendo que:
,
Vamos começar pelo eixo AB
=26,46 mm
Passo 2
Então agora seguimos para o eixo BC!
=16,667 mm
Resposta
Então gurizada, os menores diâmetros para as tensões mínimas de cisalhamento, são e .
Exercícios de Livros Relacionados
O eixo maciço de 32mm de diâmetro é usado para transmitir os torques aplicados às engrenagens. Se o eixo estiver apoiado em mancais lisos em A e B , que não resistem a torque, determine a tensão de ci
O eixo maciço com 60mm de diâmetro está sujeito aos carregamentos de torção distribuídos e concentrados mostrados na figura. Determine as tensões de cisalhamento máxima e mínima no eixo e especifique
O tubo de cobre tem diâmetro externo de 62,5mm e diâmetro interno de 57,5mm . Se estiver firmemente preso à parede em C e for submetido a um torque uniformemente distribuído, como mostra a figura, det
O eixo maciço está preso ao suporte em C e sujeito aos carregamentos de torção mostrados. Determine a tensão de cisalhamento nos pontos A e B e faça um rascunho da tensão de cisalhamento nos elementos
A haste tem diâmetro de 12mm e peso de 80N/m . Determine a tensão de torção máxima provocada na haste pelo seu peso em uma seção localizada em A .