Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 48
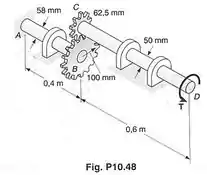
Dois eixos maciços são conectados pelas duas engrenagens mostradas. Usando , determinar a energia de deformação em cada um dos eixos, quando um torque de é aplicado em .
Passo 1
Faaala, meus chuchus! Tudo bem? Vamos fazer uma questão de energia de deformação para arrasar na prova?
A questão pede que a gente calcule a energia de deformação da barra e a energia de deformação da barra . Essas duas barras estão conectadas por engrenagens. A barra é girada com um torque , fazendo a barra girar com um torque .
Supomos que as duas barras estão girando tão devagar que estão em equilíbrio!
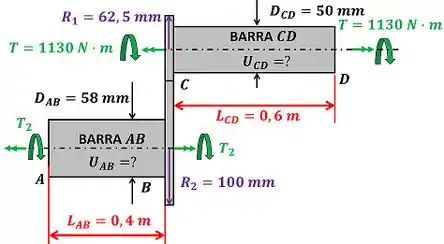
e são os diâmetros das barras e respectivamente. e são os raios da engrenagem da barra e respectivamente. e são os comprimentos das barras e respectivamente.
Na figura, vemos que a barra torce com um torque constante e a barra torce com um torque constante . Para calcular e através desses torques, usamos a equação 10.22 do livro. Essa equação serve para barras com áreas constantes e torques constantes, como é nosso caso.
é o módulo de elasticidade transversal do material das barras. Ele vale segundo o enunciado.
Agora que temos todas essas fórmulas, vamos começar a fazer as contas, calculando o valor do torque !
Passo 2
Para achar o torque temos que lembrar da terceira lei de Newton chamada de ação e reação. Levando essa lei em conta, vemos que a engrenagem da barra empurra a engranagem da barra com uma força e a engrenagem da barra reage empurrando a engrenagem da barra com uma força igual e oposta!
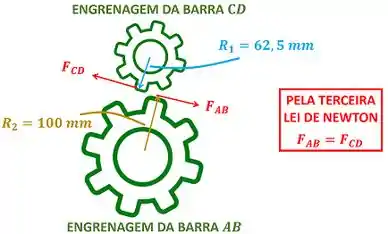
Como os torques são iguais às forças divididas pelos raios , concluímos que:
Agora só falta achar os momentos de inércia polares e para a gente calcular e .
Passo 3
Antes de achar as energias de deformação e de cada barra, temos que encontrar os valores dos momentos de inércia polares e de cada barra
Achamos e , através das fórmulas de momentos de inércia polares para áreas circulares abaixo. Antes, devemos converter os diâmetros de pra , multiplicando eles por .
Com esses valores podemos partir para nosso passo final!
Passo 4
Substituímos , e nas equações de , e para achar as energias de deformação. No entanto, antes disso converter o de para , multiplicando por .
Maravilha! Acabamos com a questão! :-D