Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 100
Usando as informações fornecidas no Apêndice , calcular o trabalho realizado pelas cargas, tal como elas são aplicadas na viga:
- se a carga é aplicada inicialmente;
- se o momento é aplicado inicialmente.
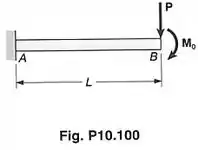
Passo 1
Oi, gente! Tudo bem com vocês? Bora fazer um exercício de cálculo de trabalho realizado por uma força e um momento sobre uma viga que se deforma?
Temos que calcular o trabalho em duas situações. Na situação (a), temos que calcular o trabalho , quando a força é aplicada primeiro. é aumentada até fazer o ponto se deslocar e ficar com um ângulo de inclinação . Depois, o momento é aplicado até fazer o ponto se deslocar mais e até aumentar ângulo de inclinação em .
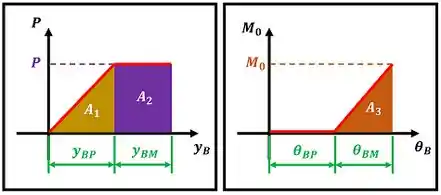
Na figura acima podemos ver como e variam conforme as deformações aumentam. Abaixo das curvas vermelhas podemos ver as áreas coloridas , e . O trabalho é a soma dessas áreas que estão sob as curvas das cargas.
Na situação (b), o momento é aplicado primeiro. é aumentado até fazer o ponto se deslocar e ficar com um ângulo de inclinação . Depois, a força é aplicada até fazer o ponto se deslocar mais e até aumentar ângulo de inclinação em .
A figura abaixo mostra as curvas e áreas formadas na situação (b).
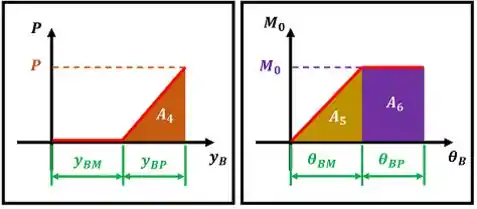
Na situação (b), temos que calcular o trabalho que também é igual à soma as áreas abaixo das curvas das cargas.
Para calcular todas as 6 áreas, precisamos saber quanto valem , , e . Para encontrar equações de , , e usamos o apêndice do livro.
Vamos fazer isso no próximo passo.
Passo 2
As equações de e são encontradas, quando consideramos que só existe um carregamento deformando a viga: a força . Nesse caso, o tipo de viga e carregamento é o tipo 1 da tabela desse apêndice. Logo:
Já as equações de e são obtidas, quando consideramos que só existe um carregamento deformando a viga: o momento . Nesse caso, o tipo de viga e carregamento é o tipo 3 da tabela desse apêndice. Logo:
Com essas equações, somos capazes de achar todas as áreas no próximo passo.
Passo 3
Então é isso, galera. Só falta aprender a calcular as 6 áreas a partir de , , e que resolvemos a equação. Aprendemos isso, olhando para os gráficos do primeiro passo.
No primeira figura vemos que é um triângulo de base e altura , é um retângulo de lados e e é um triângulo de base e altura . Por isso:
Substituindo essas áreas na equação de , achamos:
Aeee! Achamos a resposta da letra (a) da questão!
Vamos partir pra letra (b) agora!
Passo 4
No segunda figura vemos que é um triângulo de base e altura , é um triângulo de base e altura e é um retângulo de lados e .
Substituindo essas áreas na equação de , achamos:
Prooonto! Achamos a resposta da letra (b) e acabamos com a questão! Perceba que a resposta da letra (a) é igual à resposta da letra (b)!