Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 96
Na montagem mostrada, o membro é uma barra maciça de aço de de diâmetro e todos os outros membros são feitos de aço de . Usando-se , determinar a deflexão do ponto , provocada pela carga de .
Passo 1
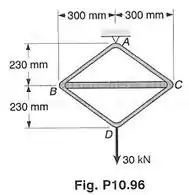
Faaaala, meus chuchus! Prontos para uma questão de cálculo de deflexão através do método de energia? Pode não parecer, mas essa questão é uma questão de treliça. A única diferença em relação a questões de treliça tradicionais é que, dessa vez, os membros terão áreas de seção transversal diferentes por conta de seus diâmetros diferentes.
O enunciado mostra uma figura com 5 membros da treliça (, , , e ) e quer que a gente calcule a deflexão do ponto produzida pela força que é aplicada em .
Como temos que usar o método da energia, vamos calcular a partir da equação que calcula a quantidade de energia que é absorvida pela treliça, quando ela se deforma.
é a energia total absorvida pela treliça. Logo, é a soma das energias absorvidas por cada treliça. Isso é mostrado pela equação abaixo.
Para calcular cada uma dessas energia, vamos precisar calcular as forças aplicadas a cada um dos membros da treliça! A figura abaixo mostra as forças que são aplicadas a cada membro mais a força e a força de reação do ponto .
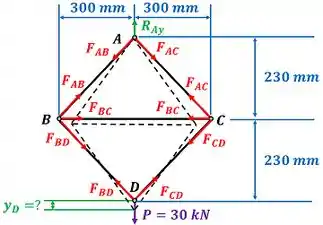
Para encontrar as energias de cada membro da treliça, usaremos a equação 10.14 que calcula a energia absorvida por uma barra de comprimento e área de seção transversal , quando ela sofre a ação de uma força axial .
Agora podemos começar os cálculos no próximo passo.
Passo 2
Para encontrar as forças , , , e , precisamos calcular a reação da restrição do ponto .
Para fazer esses cálculos, vamos usar o diagrama de corpo livre da treliça inteira abaixo.
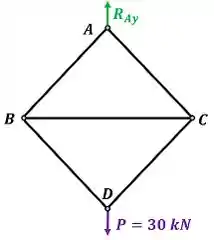
Vamos fazer o equilíbrio de forças na treliça inteira. Esse equilíbrio diz que a soma de todas as forças em vale zero. Como a força está apontando pra baixo, ela ganhará um sinal de menos na equação.
Pronto! Achamos a força de reação! Agora somos capazes de achar as forças , , , e aplicadas nos membros da treliça.
Passo 3
Para facilitar nossa vida na hora de achar essas forças, podemos observar que as forças e a treliça são simétricas. Vamos observar a imagem abaixo para ver os planos de simetria representados em vermelho.
Por conta dessa simetria, as seguintes forças são iguais.
Agora, podemos achar , , e , fazendo o equilíbrio de forças no ponto .
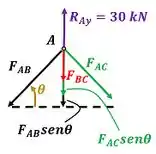
Antes, temos que lembrar que, no equilíbrio de forças em , as forças que apontam pra baixo devem ganhar um sinal de menos na frente.
O equilíbrio de forças em resulta em:
Logo:
Agora podemos achar a força restante, fazendo o equilíbrio das forças em do ponto .
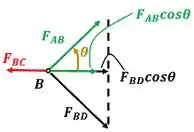
Temos que lembrar antes, que no equilíbrio em , todas as forças apontando pra esquerda ganham um sinal de menos na frente.
Para achar o e o e conseguir calcular o valor das forças, recorremos ao desenho abaixo. Nele, vemos que , , e foram calculados usando o teorema de Pitágoras com os comprimentos de e como catetos.
Substituindo nas equações das forças:
Agora podemos achar as energias de cada membro da treliça.
Passo 4
Para achar as energias , , , e dos membros, usamos as forças que calculamos na equação de energia do passo 1.
As áreas das seções transversais de cada membro da treliça está presente na fórmula das energias. Logo precisamos achar esses valores a partir dos diâmetros informados.
Como os diâmetros , , e são iguais:
Já para temos:
Antes, precisamos converter de pra multiplicando por , converter de pra multiplicando por , converter de pra multiplicando por e converter de pra multiplicandp por .
Com esse valores, podemos calcular e no próximo passo.
Passo 5
Somando todas as energias de cada membro da treliça, achamos .
é encontrado a partir da fórmula que deduzimos no passo 1.
Boooooa, meus queridos! Chegamos na resposta da questão!