Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 103
Para a viga e carregamento mostrado, pede-se:
- calcular o trabalho realizado pelas cargas, enquanto elas são aplicadas sucessivamente na viga, usando as informações do Apêndice ;
- calcular a energia de deformação da viga, pelo método da Sec. 10.4, e mostrar que isto é igual ao trabalho obtido na parte a.
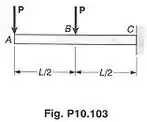
Passo 1
Oi, galerinha! Como vocês estão? Bora fazer um exercício de cálculo de trabalho realizado por forças sobre uma viga que se deforma?
Temos que calcular o trabalho de duas formas. Na forma (a), temos que calcular o trabalho , quando a força do ponto é aplicada primeiro. é aumentada até fazer o ponto se deslocar . Além disso, essa força faz o ponto se deslocar . Depois, a força do ponto é aplicada até fazer o ponto se deslocar mais . Essa força também faz o ponto se deslocar mais .
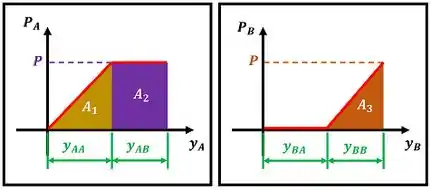
Na figura acima podemos ver como e variam conforme as deformações aumentam. Abaixo das curvas vermelhas podemos ver as áreas coloridas , e . O trabalho é a soma dessas áreas que estão sob as curvas das cargas.
Para calcular essas 3 áreas, precisamos saber quanto valem , , e . Para encontrar equações de , , e usamos o apêndice do livro.
A forma (b) de se calcular o trabalho é resolvendo a integral do momento fletor abaixo.
onde é o módulo de elasticidade do material da viga e é o momento de inércia do perfil da viga.
Depois de receber todas essas informações, estamos prontos pra começar a calcular o trabalho da forma (a) no passo seguinte!
Passo 2
As equações de e são encontradas, quando consideramos que só existe um carregamento deformando a viga: a força . Nesse caso, o tipo de viga e carregamento é o tipo 1 da tabela desse apêndice. Logo:
Já as equações de e são obtidas, quando consideramos que só existe um carregamento deformando a viga: a força . Nesse caso, o tipo de viga e carregamento é o tipo 1 da tabela desse apêndice. No entanto, para achar , teremos que considerar que a viga tem metade do tamanho, porque a força é aplicada a uma distância do engaste. Logo:
Para achar vamos precisar usar uma aproximação. Vamos considerar que o deslocamento em produzido pela força em é a soma do deslocamento de em relação ao engaste com o deslocamento do ponto em relação ao ponto .
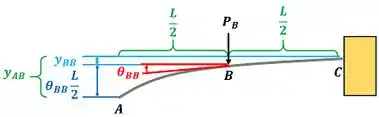
é o ângulo de inclinação da viga em causado pela força . Ele também é encontrado no apêndice para o tipo 1 da tabela. Usando na equação de :
Com essas equações, somos capazes de achar todas as áreas no próximo passo.
Passo 3
Então é isso, galera. Só falta aprender a calcular as 3 áreas a partir de , , e que resolvemos a letra (a) da questão. Aprendemos isso, olhando para os gráficos do primeiro passo. No primeira figura vemos que é um triângulo de base e altura , é um retângulo de lados e e é um triângulo de base e altura . Por isso:
Substituindo essas áreas na equação de , achamos:
Aeee! Achamos a resposta da letra (a) da questão!
Vamos partir pra letra (b) agora!
Passo 4
Para achar o trabalho , temos que resolver uma integral que tem o momento fletor da viga. Isso quer dizer que precisamos achar pra achar . Fazemos isso, dividindo a viga em duas partes (uma esquerda e outra direita). O será encontrando calculando o equilíbrio de momentos da parte esquerda da viga. Se a parte esquerda incluir apenas a força teremos:
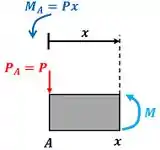
Faremos o equilíbrio dessa parte esquerda em relação ao ponto . A equação de equilíbrio de momentos diz que a soma dos momentos deve valer zero.
Conseguimos achar um valor para , mas tem um segundo valor. Quando a parte esquerda da viga inclui a força , esse momento fletor passa a ter outro valor.
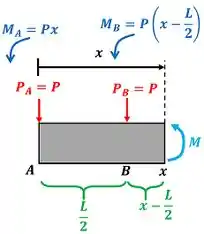
Pronto, com os dois valores de estamos aptos a encontrar !
Passo 5
tem dois valores. Um quando vale entre e e outro, quando vale entre e .
Por isso, para substituir na integral que calcula , precisamos separar a integral em duas. Uma que vai de a para o primeiro valor de e outra que vai de a para o segundo valor de .
Substituindo os valores de nas integrais corretas, achamos:
Colocando as constantes para fora da integral, achamos:
Uhuuul! Achamos a letra (b) da questão! Arrasamos!