Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 42

Dois eixos de seção transversal cheia, cada um com 30 mm de diâmetro, são conectados pelas engrenagens mostradas. Sabendo que G=77,2 GPa, determine o ângulo que extremidade em A descreve quando um torque de intensidade T =   200 N ⋅ m é aplicado nela.

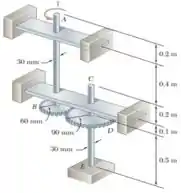
Passo 1

Muito bem, esta vai ser interessante gurizada, vamos começar pelos cálculos de torque, partiu!!!:

Força circunferencial das engrenagens B e D:

F = T A B r B = T D E r D

T D e = r D r B T A B = 90 60 200 = 300   N ⋅ m

Agora, a torção do eixo DE:

J D E = π 2 c 4 = π 2 0.015 4 = 70.522 × 10 - 9   m 4 L D E = 0.5   m

φ D E = T D E L D E G J D E = 300 0.5 77.2 × 10 - 9 79.522 × 10 - 9 = 24.434 × 10 - 3   r a d

Passo 2

Rotação em D:

φ D = φ D E = 24.434 × 10 - 3   r a d

Agora, antes de continuarmos, precisamos saber a fórmula da rotação diferencial das engrenagens:

δ = r D φ D = r B φ B

Continuando, a rotação na engrenagem B:

φ B = r D r B φ D = 90 60 24.434 × 10 - 3 = 36.651 × 10 - 3   r a d

Agora vamos pra torção do eixo AB:

L A B = 0.1 + 0.2 + 0.4 + 0.2 = 0.9   m J A B = 79.522 × 10 - 9   m 4

φ A B = T A B L A B G J A B = 200 0.9 77.2 × 10 9 79.522 × 10 - 9 = 29.320 × 10 - 3   r a d

Passo 3

A rotação em A:

φ A = φ b + φ A B = 36.651 × 10 - 3 + 29.320 × 10 - 3 r a d   = 65.971 × 10 - 3   r a d

Ângulo em A:

A = r a d × 180 π   =   65.971 × 10 - 3 × 180 π = 3.79 º

Resposta

3,79°

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois eixos maciços de aço ( G = 77G P a ) são conectados pelas engrenagens mostradas. Determinar o ângulo de torção da extremidade A, quando nesse ponto um torque T de 340N . m é aplicado.
Dois eixos maciços de aço ( G = 77G P a ) são conectados pelas engrenagens mostradas. Determinar o ângulo de torção da extremidade A, quando nesse ponto um torque T de 340N . m é aplicado.
Um eixo circular maciço de transmissão, de 1,5 m de comprimento, está sujeito a um torque de 12Kn.m. Determinar o diâmetro necessário do eixo, sabendo-se que o ângulo de torção não deve exceder a 1,5
Para o sistema eixo-engrenagem do Prob. 3.33, determinar: (a) o máximo valor permissível de T, se o ângulo de torção entre C e D não exceder a 0,75 ° ; (b) o correspondente valor do ângulo de torção,
Um furo é puncionado em A, numa chapa plástica, por uma força P de 600N aplicada na extremidade D da alanaca CD, que está rigidamente ficada a um eixo cilíndrico maciço BD. As especificações de projet