Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas de Revisão - Ex. 153

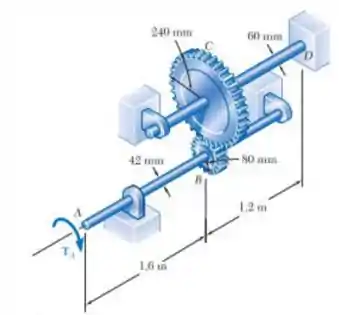
Dois eixos de seção transversal cheia estão acoplados por engrenagens, conforme mostra a figura. Sabendo que G = 77,2   G P a para cada eixo, determine o ângulo de torção de rotação da extremidade A quando T A = 1200   N * m .

Passo 1

E ai gurizada tudo certinho? O enunciado pede que a gente determine o ângulo de torção de rotação da extremidade A quando T A = 1200   N * m . Então vem comigo ;)

Força de contato circunferencial entre as engrenagens B e C:

F = T A B r B = T C D r C           T C D = r C r B T A B T A B = 1200   N * m        

T C D = 240 80   x   1200 = 3600   N * m  

Torção no eixo CD: c = 1 2 d = 0,030   m ,     L = 1,2   m ,       G = 77,2   x   10 9 P a J = π 2 c 4 = π 2   x   0,030 4 = 1,27234   x   10 - 6   m 4 φ C / D = T L G J = 3600   x   ( 1,2 ) 77,2   x   10 9   x   ( 1,27234   x   10 - 9 ) = 43,981   x   10 - 3   r a d

Ângulo de rotação em C. φ c = φ C / D = 43,981   x   10 - 3   r a d

Passo 2

Deslocamento circunferencial nos pontos de contato das engrenagens B e C:

δ = r C φ C = r B φ B

Ângulo de rotação a B. φ B = r C r B φ C = 240 8   x   43,981   x   10 - 3 = 131,942   x   10 - 3 r a d

Torção no eixo AB: c = 1 2 d = 0,021 m ,     L = 1,6   m ,     G = 77,2   x   10 9 P a

J = π 2 c 4 = π 2   x   0,021 4 = 305,49   x   10 9   m 4 φ A / B = T L G J = 1200   x   ( 1,6 ) 77,2   x   10 9   x   ( 305,49   x   10 - 9 ) = 81,412   x   10 - 3   r a d

Ângulo de rotação em C. φ A = φ B + φ A / B = 213,354   x   10 - 3   r a d

Resposta

φ A = 12,22 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um eixo é submetido a um torque T . Compare a efetividade da utilização do tubo mostrado na figura com a de uma seção maciça de raio c . Para isso, calcule o aumento percentual na tensão de torção e n
As hélices de um navio estão acopladas a um eixo maciço de aço A-36 com 60 m de comprimento, diâmetro externo de 340 mm e diâmetro interno de 260 mm. Se a potência de saída for 4,5 MW quando o eixo gi
O eixo de transmissão tubular para a hélice de um aerodeslizador tem 6 m de comprimento. Se o motor transmitir 4 MW de potência ao eixo quando as hélices giram a 25 rad/s, determine o diâmetro interno
O eixo de aço A-36 é composto pelos tubos A B e C D e uma seção maciça B C . Está apoiado em mancais lisos que permitem que ele gire livremente. Se as engrenagens, presas às extremidades do eixo, fore
As extremidades estriadas e engrenagens acopladas ao eixo de aço A-36 estão sujeitas aos torques mostrados. Determine o ângulo de torção da engrenagem C em relação à engrenagem D . O eixo tem diâmetro