Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 50
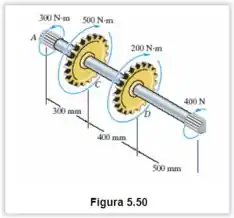
As extremidades estriadas e engrenagens acopladas ao eixo de aço A-36 estão sujeitas aos torques mostrados. Determine o ângulo de torção da engrenagem em relação à engrenagem . O eixo tem diâmetro de .
Passo 1
Olá, galera! E aí, vamos resolver esse problema?
Por esse eixo está sobre esforços de torção, ele vai sofrer uma deformação que chamamos de ângulo de torção.
O enunciado pede que seja determinado o ângulo de torção da engrenagem em relação à engrenagem , e nos fornece esses dados:
Aço A-36, portanto,
O ângulo de torção de um ponto do eixo em relação a um ponto desse mesmo eixo é dado por essa fórmulinha:
Onde é a distância entre esses pontos, é o módulo de cisalhamento do material em questão, é o momento polar de inércia do eixo, e é o torque interno entre esses dois pontos, ou seja, em .
Percebe que a gente já tem e . Mas não tem e . Bora então começar achando o torque em . Vamos lá!
Passo 2
Para achar o torque num trecho de um eixo, a gente faz uma seção nesse trecho e olha só para um dos lados, posiciona o torque, e acha o valor dele através do equilíbrio.
Para o nosso caso, vamos fazer uma seção em , e olhar para a extremidade que tem o ponto (você poderia olhar para o outro lado também, se quiser, tá?) O diagrama de corpo livre dessa situação que a gente descreveu fica:
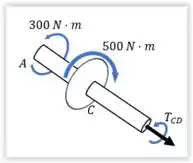
Aí pelo equilíbrio, vamos ter
Passo 3
Aí lembra que para encontrar o ângulo de torção, utilizaremos a fómula:
O momento polar de inércia, , é dado por essa expressão, já que o eixo não é vazado:
Substituindo na fórmula do ângulo de torção, temos:
Passo 4
Como , podemos substituir os dados fornecidos aí e achar o ângulo:
Convertendo para graus: