Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 81
Uma unidade de isolamento de vibrações consiste em dois blocos de borracha dura colados a uma placa AB e a suportes rígidos conforme mostrado. Sabendo que a intensidade da força produz uma deflexão na placa AB, determine o módulo de rigidez da borracha utilizada.
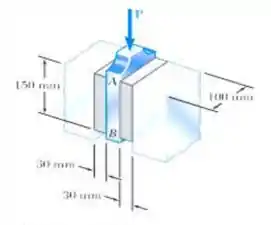
Passo 1
Fala aí gurizada tudo belezinha?? O enunciado pede para que a gente determine o determine o módulo de rigidez o elemento, vamos antes desenhar um diagrama de corpo livre :D
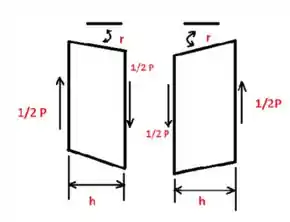
Agora gurizada precisamos determinar a força P indicada no desenho esboçado acima:D
Agora sim podemos determinar a tensão de cisalhamento
O enunciado nos fornece os seguintes dados, a partir destes podemos determinar o modulo de elasticidade:
Resposta
Exercícios de Livros Relacionados
A figura mostra a porção elástica do diagrama tensão – deformação de cisalhamento para um aço – liga. Se um parafuso de 6 m m de diâmetro feito desse material for utilizado em uma junta sobreposta, de
Um bloco cilíndrico curto de bronze C86.100, com diâmetro original de 38m m e comprimento de75m m , é colocado em uma máquina de compressão e comprimido até atingir o comprimento de 74,5m m . Determin
A figura mostra a porção elástica do diagrama tensão - deformação para um aço-liga. O corpo de prova do qual ela foi obtida tinha diâmetro original de 13m m e comprimento de referência de 50m m . Se u
O bloco de borracha é submetido a um alongamento de 0,75 m m ao longo do eixo x , e suas faces verticais sofrem uma inclinação de modo que θ = 89,3 ° . Determine as deformações ϵ x , ϵ yeγ x y . Consi
Um material macio está confinado no interior de um cilindro rígido que repousa sobre um suporte rígido. Considerando que ϵ x =0 e ϵ y=0 , determine qual será o fator de aumento do módulo de elasticida