Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 55

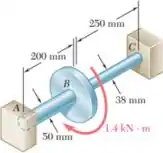
Dois eixos de seção transversal cheia, feitos de aço G = 77 , 2   G P a , são conectados a um disco de acoplamento B e engastados ao suporte rígido em A e C. Para o carregamento mostrado, determine (a) a reação de cada suporte, (b) a tensão de cisalhamento máximo no eixo AB e (c) a tensão de cisalhamento máximo no eixo BC.

Passo 1

E ai galerinha, o exercício pede para que a gente determine a reação e a tensão de cisalhamento nos eixos, então vamos começar trazendo as informações ...

T = T A B L A B = 0.200   m c = 1 2 d = 25   m m = 0.025   m

Para determinarmos o valor de J A B   temos a seguinte equação:

J A B = π 2 c 4 = π 2 0.025 4 = 613.59 × 10 - 9 m 4 φ B = T A B L A B G J A B

T A B = G J A B L A B φ B = 77.2 × 10 9 613.59 × 10 - 9 0,200 φ B = 236.847 × 10 3 φ B

Passo 2

Seguimos para o eixo BC, então vamos começar trazendo as informações ...

T = T B C L B C = 0.250   m   c = 1 2 d = 19   m m = 0.19   m

Para determinarmos o valor de J B C   temos a seguinte equação:

J B C = π 2 c 4 = π 2 0.019 4 = 204.71 × 10 - 9   m 4 φ B = T B C L B C G J B C

E para o torque temos:

T B C = G J B C L B C φ B = 77.2 × 10 9 204.71 × 10 - 9 0.250 = 63.214 × 10 3 φ B

Agora calculamos o equilíbrio do disco de acoplamento, temos que realizar o somatório dos torques em ambos os eixos

T = T A B + T B C

1.4 × 10 3 = 236.487 × 10 3 φ B + 63.214 × 10 3 φ B φ B = 4.6657 × 10 - 3 r a d

T A B = 236 , 847 × 10 3 40 6657 × 10 - 3 = 1.10506 × 10 3 N / m

T B C = 63 , 214 × 10 3 4 , 6657 × 10 - 3 = 294 , 94   N / m

Passo 3

Calculando a tensão máxima AB:

τ A B = T A B c J A B = 1.10506 × 10 3 0.025 613.59 × 10 - 9 = 45   × 10 6   P a

E por fim, calculamos o (c), a tensão máxima BC:

τ B C = T B C c J B C = 294.94 0.019 204.71 × 10 - 9 = 27 , 4 × 10 6   P a

Resposta

  1. T A = T A B = 1105   N / m ;
  2. T B = T B C = 295   N / m ;
  3. τ A B = 45 , 0     M P a e τ B C = 2 7 , 4     M P a .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo de aço A-36 é composto pelos tubos A B e C D e uma seção maciça B C . Está apoiado em mancais lisos que permitem que ele gire livremente. Se as engrenagens, presas às extremidades do eixo, fore
O eixo de aço A-36 de 20m m de diâmetro é submetido aos torques mostrados. Determine o ângulo de torção da extremidade B .
Um eixo é submetido a um torque T . Compare a efetividade da utilização do tubo mostrado na figura com a de uma seção maciça de raio c . Para isso, calcule o aumento percentual na tensão de torção e n
As hélices de um navio estão acopladas a um eixo maciço de aço A-36 com 60 m de comprimento, diâmetro externo de 340 mm e diâmetro interno de 260 mm. Se a potência de saída for 4,5 MW quando o eixo gi
O eixo de transmissão tubular para a hélice de um aerodeslizador tem 6 m de comprimento. Se o motor transmitir 4 MW de potência ao eixo quando as hélices giram a 25 rad/s, determine o diâmetro interno