Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 56

Resolvido o problema 3.55 assumindo que o eixo AB é substituído por um eixo vazado de mesmo diâmetro externo e 25 mm de diâmetro interno.

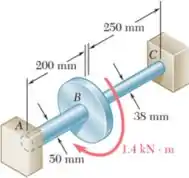
Passo 1

Muito bem galerinha, como vimos no enunciado desta questão, usaremos os dados da questão 3.55 e alteraremos os dados do eixo, vamos aos cálculos:

Eixo AB:

T = T A B   L A B = 0.200 c 2 = 25   m m = 0.025   m c 1 = 12,5   m m   = 0.0125   m

Calculando J A B temos:

J A B = π 2 c 2 4 - c 1 4 = π 2 0.025 4 - 0.0125 4 = 575.24 × 10 - 9   m 4

E para o cálculo do torque temos T A B

T A B = G J A B L A B φ B = 77.2 × 10 9 575.24 × 10 - 9 0.200 φ B = 222 , 04 × 10 3 φ B

Passo 2

Para o eixo BC temos:

T = T B C L B C = 0 , 250   m c = 1 2 d = 19   m m = 0 , 019   m

Calculando J B C temos:

J B C = π 2 c 4 = π 2 0 , 019 4 = 204 , 71 × 10 - 9 m

E para o cálculo do torque temos T B C

T B C = G J B C L B C φ B = 77.2 × 10 9 204.71 × 10 - 9 0.250 φ B = 63 , 214 × 10 3 φ B

Agora calculamos o equilíbrio do disco de acoplamento realizando o somatório dos torques:

T = T A B + T B C

T = 1 , 4 × 10 3 = 222 , 04 × 10 3 φ B + 63 , 214 × 10 3   N / m

φ B = 4 , 9079 × 10 - 3   r a b

T A B = 222 , 04 × 10 3 4 , 9079 × 10 - 3 = 1 , 08975 × 10 3   N / m

T B C = 63 , 214 × 10 3 4 , 9079 × 10 - 3 = 310 , 25   N / m

Passo 3

Calculando a tensão máxima AB:

τ A B = T A B c 2 J A B = 1.08975 × 10 3 0.025 575.243 × 10 - 9 = 47 , 4 × 10 6   P a

E por fim, calculamos a tensão máxima BC:

τ B C = T B C c J B C = 310.25 0.019 204.71 × 10 - 9 = 28 , 8 × 10 6   P a

Resposta

  1. T A = T A B = 1090   N / m ;
  2. T C = T B C = 310   N / m ;
  3. τ A B = 47.4   M P a e τ B C = 28.8   M P a .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra de seção circular com 914,4m m de comprimento tem um diâmetro de 63,5m m e é feita de aço doce considerado elastoplástico com T E = 144,8M P a e G = 77,2G P a . Determine o torque necessário
Um barra de seção cheia de 31,8m m de diâmetro é feita de um material elastoplástico com t E = 34,5M P a Sabendo que o núcleo elástico da barra tem um diâmetro de 25,4 m m , determine
Um cilindro de 50 mm de diâmetro de 30 in. de diâmetro é feito de latão para qual o diâmetro tensão-deformação está apontado. Sabendo que o ângulo de giro é de 5° em um comprimento de 725 mm, determin
O torque T causa uma rotação de 0,6° na extremidade B da barra de alumínio mostrada, Sabendo que b = 15m meq u eG = 26G P a , determine a máxima tensão de cisalhamento na barra.
Cada uma das barras de latão mostradas é sujeita a um torque de intensidade T = 12,5k i p . i n . Sabendo que G = 5,6x10 6 p s i , determine para cada barra a máxima tensão de cisalhamento e o ângulo