Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 73

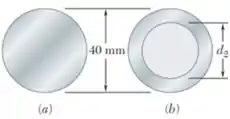
O projeto de um elemento de máquina especifica um eixo com diâmetro externo de 40 mm para transmitir 45 kW. (a) Se a rotação for de 720 rpm, determine a tensão de cisalhamento máxima no eixo a. (b) Se a rotação do eixo pode ser aumentada em 50% passando a 1080 rpm, determine o maior diâmetro interno do eixo b para o qual a tensão de cisalhamento máxima será a mesma em cada eixo.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine a a tensão de cisalhamento máxima no eixo a e o maior diâmetro interno do eixo b. Vamos aos nossos cálculos:

Primeiramente temos que determinar a frequência

f = 720 60 = 12 H z

Sendo a potência dada por P = 45   k W = 45 × 10 3   w podemos então determinar o torque:

T = P 2 π f = 45 × 10 3   2 π 12 = 596.83   N / m

O diâmetro do elemento é de:

c = 1 2 d = 20   m m = 0.020   m

Agora sim gurizada podemos determinar a tensão :D

τ = T c J = 2 T π c 3 2 596.83 π 0.020 3 = 47.494 × 10 6   P a

τ m a x = 47.5   M P a

Passo 2

Primeiramente temos que determinar a frequência

f = 1080 60 = 18   H z

Então vamos determinar o torque

T = 45 × 10 3   2 π 18 = 397 , 89   N / m

A partir da equação da tensão podemos determinar o diâmetro, venham comigo que está quase no final :D

τ = T c 2 J = 2 T c 2 π c 2 4 - c 1 4

Isolando c 1 4   temos:

c 1 4 = c 2 4 - 2 T c 2 π τ

c 1 4 = 0.020 4 - 2 397.89 0.020 π 47.494 × 10 6 = 53 , 333 × 10 - 9

c 1 = 15.20 × 10 - 3   m = 15 , 20   m m

d 2 = 2 c 1 = 30 , 4   m m

Resposta

  1. τ m a x = 47,5   M P a
  2. 30,4   m m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um eixo maciço tem diâmetro de 40 m m e comprimento de 1 m e é feito de um material elástico-plástico com tensão de escoamento τ e = 100 M P a . Determine o torque elástico máximo T e e o ângulo de to
Um eixo maciço com diâmetro de 50 m m é feito de material elástico-plástico com tensão de escoamento τ e = 112M P a e módulo de cisalhamento G = 84G P a . Determine o torque exigido para desenvolver u
O eixo é submetido a um torque T que produz escoamento na superfície do segmento de maior diâmetro. Determine o raio do núcleo elástico produzido no segmento de menor diâmetro. Despreze a concentração
O eixo é composto por duas seções rigidamente acopladas. Se o material for elástico perfeitamente plástico como mostra a figura, determine o maior torque T que pode ser aplicado eixo. Além disso, dese
O eixo é feito de um material elástico perfeitamente plástico como mostra a figura. Faça um gráfico da distribuição da tensão de cisalhamento que age ao longo de uma linha radial se o eixo for submeti