Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas de Revisão - Ex. 129

Dois eixos sólidos de aço são conectados pelas engrenagens mostradas. Utilizando o método do trabalho e energia, determine o ângulo de rotação que descreve a extremidade em D quando T = 820   N ∙ m . Utilize G = 77,2   G P a .

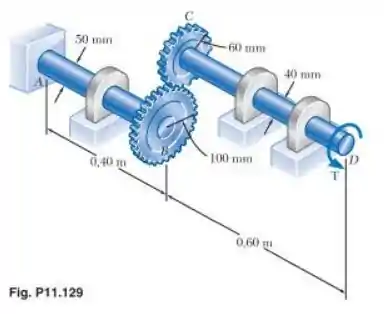
Passo 1

Fala, galerinha. Beleza? Bora pra mais um exercício.

Primeiro, vamos determinar o momento polar de inércia:

J = π 2 c 4

Onde:

c = d 2 = 40 2 = 0,020   m

Portanto, o momento polar de inercia vai ser:

J = π 2 0,020 4 J = 251,33 × 10 - 9   m 4

Então, a energia de deformação no eixo C D vai ser dada por:

U C D = T 2 L 2 G J U C D = 820 2 0,60 2 77,2 × 10 9 251,33 × 10 - 9 U C D = 10,397   J

Passo 2

Em seguida, podemos utilizar a relação de semelhança entre os eixos A B e C D a fim de determinarmos a torção em A B . Fica assim:

T A B r B = T C D r C T A B 0,06 = 820 0,100 T A B = 1366,67   N ∙ m

Assim, vamos determinar o momento polar de inercia para o eixo A B vai ser:

J = π 2 c 4

J = π 2 0,025 4 J = 613,59 × 10 - 9   m 4

E então, a energia de deformação neste mesmo eixo é dada por:

U A B = T 2 L 2 G J U A B = 1366,67 2 0,40 2 77,2 × 10 9 613,59 × 10 - 9 U A B = 7,886   J

Passo 3

Por fim, vamos lembrar que a a energia de deformação é uma grandeza escalar, portanto, a máxima energia de deformação vai ser a soma das energias de deformação. Fica assim:

U = U A B + U C D U = 18,283   J

Portanto, temos que o ângulo de rotação vai ser:

1 2 T θ = U θ = 2 U T = 2 18,283 820 θ = 2,55 °

É isso, galera Bora pra próxima?

Resposta

θ = 2,55 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o Prob. 10.14, usando as propriedades do material dado e assumindo que a barra A B C é feita inteiramente de:aço;alumínio.
Uma barra uniforme de 9,5m m de diâmetro e 2,7m de comprimento é feita de um aço inoxidável de alta resistência, para o qual σ e = 860M P a e E = 190G P a .Sabendo-se que uma energia de deformação de
Uma barra A B de 6m m de diâmetro, com comprimento L = 2,5m é feita de uma liga de alumínio para a qual σ e = 320M P a e E = 72G P a . Sabendo-se que uma energia de deformação de 10J deve ser absorvid
Resolver o Prob. 10.19, assumindo que a = 635m m .
A barra A B C é feita de aço ára o qual σ e = 350M P a e E = 200G P a . Sabendo-se que uma energia de deformação de 4,5N ⋅ m deve ser acumulada pela barra assim que a carga axial P é aplicada, determi