Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 139
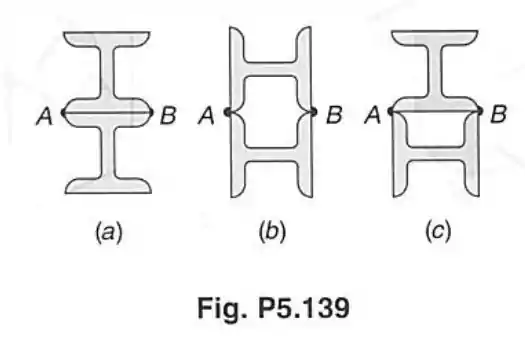
Dois perfis laminados de aço podem ser soldados em e , de qualquer uma das três maneiras mostradas, para formar uma viga composta. Sabendo-se que para cada uma das soldas a força cisalhante admissível horizontal é de , determinar, para cada arranjo, a máxima força cortante vertical admissível para a viga composta.
Passo 1
Primeiramente precisaremos pegar as informações desse perfil no apêndice (referência da terceira edição desse livro) e com isso nós temos que as informações mais pertinentes são:
No caso da letra temos uma situação em que a linha neutra horizontal passa pelos pontos e de forma que:
E como os dois corpos são simétricos então é um tanto fácil ver que a linha neutra onde a inércia em é nula e passa por e .
Então a inércia que nos interessará para esse caso é a inércia do eixo , já que as duas vigas estão na vertical (e a inércia que liga o centroide com o eixo neutro é uma reta vertical portanto a inércia que queremos é a inércia em por ) , logo a inércia no eixo do corpo todo será dada por:
Ou seja:
Pois o centróide dos dois corpos está a uma distância abaixo da linha neutra.
Agora o momento estático de um dos corpos vai ser calculado por:
Agora se atente a informação:
para cada uma das soldas a força cisalhante admissível horizontal é de
Essa informação se refere ao fluxo cisalhante (uma vez que solda é um ponto e ponto não tem comprimento) que passa por essas duas soldas e por serem duas nós temos que
Portanto a força cortante para uma cisalhante de será:
Isolando , pois queremos a força cortante vertical então nós temos para a letra que:
Como , então:
Passo 2
Agora para a letra temos que:
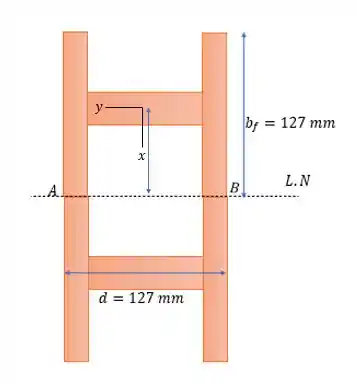
Nessa situação temos que considerar agora a inércia no eixo , já que as vigas estão deitadas em relação ao desenho dado no apêndice da terceira edição desse livro. Portanto a reta que liga o centro da viga com a linha neutra é uma reta horizontal em relação ao eixo da própria viga como se vê no desenho.
Então a inércia fica como:
A distância de se mantém a mesma uma vez que então podemos encontrar o centroide do perfil facilmente.
O momento estático é igual ao anterior e vale:
E como o fluxo de cisalhamento se mantém então a força cortante será de:
Passo 3
Agora para a situação da letra :
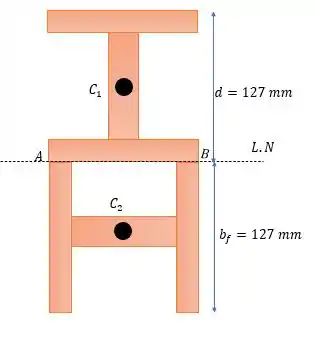
Agora nessa temos a inércia em causado pela viga que está acima da linha neutra e outra inércia em causada pela viga que está abaixo da linha neutra, dessa forma:
Uma vez que a distância dos dois centroides são iguais a , então:
O momento estático não se altera e vale:
E nem o fluxo de cisalhamento:
Portanto: