Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 89

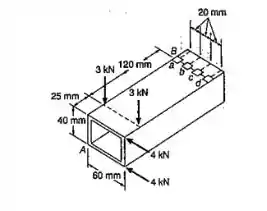
Sabendo-se que o tubo estrutural mostrado tem uma espessura de parede uniforme 6 mm, determinar a tensão normal no ponto C e a tensão de cisalhamento no ponto D.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos a figura e dizermos qual deveria ser a tensão naqueles 2 pontinhos ali. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser trazer os nossos valores pra cá pra analisar.

V x =   - 8   k N

V y =   - 6   k N

M x = - 6000 0,145 =   - 870   N . m

M y =   - 8000 0,120 =   - 960   N . m

Por ser num formato retangular, vamos pegar o retângulo maior e tirar o do meio.

A = 5,64 × 10 - 4   m ²

I x = 2,41 × 10 - 8   m 4

I y = 2,59 × 10 - 6   m 4

Q = 1,23   × 10 - 5   m 3

Passo 3

Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!

σ C = M x a I x - M y b I y = - 346,2   M P a

τ D = V y Q I x t =   - 510   M P a  

Resposta

σ C = - 346,2   M P a

τ D = - 510   M P a  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga de madeira mostrada na figura está submetida a uma força cortante vertical de 5,34 kN. Sabendo que a força cortante admissível nos pregos é 333,6 N, determine o maior espaçamento possível s dos
Uma viga com a seção transversal mostrada é submetida a uma força cortante vertical V. Determine (a) a linha horizontal ao longo da qual a tensão de cisalhamento é máxima e (b) a constante k na expres
A viga mostrada foi feita colando-se várias tábuas. Sabendo que a viga está sujeita a uma força cortante de 5 kN, determine a tensão de cisalhamento média nas juntas coladas (a) em A (b) em B.
A viga mostrada na figura foi feita pregando-se várias tábuas e está sujeita a uma força cortante de 8 kN. Sabendo que os pregos estão espaçados longitudinalmente a cada 60 mm em A e a cada 25 mm em B
Uma viga de alumínio extrudada tem a seção transversal mostrada na figura. Sabendo que a força cortante vertical na viga é 150 kN, determine a tensão de cisalhamento no (a) ponto a e (b) ponto b.