Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 46b
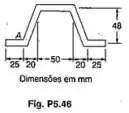
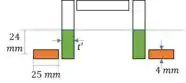
Uma placa de 4 mm de espessura é encurvada como mostrado e depois usada como uma viga. Para uma força cortante vertical de 12 kN, determinar (a) a tensão de cisalhamento no ponto A; (b) a máxima tensão de cisalhamento na viga. Esboçar também o fluxo de cisalhamento na seção transversal.
Passo 1
No passo anterior a gente já calculou o centroide e o momento de inércia!
Então só nos resta calcular o momento estático:
Passo 2
Agora é só aplicar a equação da tensão de cisalhamento:
Aplica os valores:
E prontinho:
Resposta
Exercícios de Livros Relacionados
Uma força de 12 kN é aplicada à extremidade livre da viga em balanço AB, na direção perpendicular ao eixo longitudinal da viga. Determinar o valor do ângulo para que a tensão normal no ponto b seja ze
Três forças são aplicadas a um perfil de aço laminado W250 X 49,1, como mostrado. Determinar as tensões normal e de cisalhamento nos pontos A e B.
Três forças são aplicadas a um perfil de aço laminado W250 X 49,1, como mostrado. Determinar as tensões normal e de cisalhamento nos pontos C e D.
Três placas de aço, cada uma com 12,5 mm de espessura, são soldadas juntas para formar uma viga em balanço. Para o carregamento mostrado, determinar as tensões normal e de cisalhamento nos pontos D e
Uma força de 12 kN é aplicada à extremidade livre da viga em balanço AB, na direção perpendicular ao eixo longitudinal da viga. Determinar a tensão no ponto A para quando o ângulo é 0 e para quando é