Enunciado
Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 1.Problemas - Ex. 17
Obtenha a lei do cosseno da trigonometria plana interpretando o produto (A - B) . (A - B) e a expansão do produto.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de matrizes, vetores e cálculo vetorial.
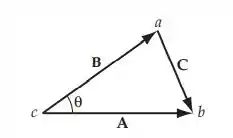
Considerando o triângulo abc, formado pelos vetores A, B e C. Temos que:
Que é a lei dos cossenos da trigonometria plana.
Resposta
Ver passo a passo.
Exercícios de Livros Relacionados
2.29. A viga deve ser içada usando-se duas correntes. Se a força resultante for de 600N , orientada ao longo do eixo y positivo, determine as intensidades das forças F AeF B que atuam em cada corrente
2.27. A resultante F R das duas forças que atuam sobre a tora deve estar orientada ao longo do eixo x positivo e ter uma intensidade de 10k N . Determine o ângulo θ do cabo acoplado a B para que a int
2.28. A viga deve ser içada usando-se duas correntes. Determine as intensidades das forças F AeF B que atuam em cada corrente, a fim de obter uma força resultante de 600N orientada ao longo do eixo y
2.26. A tora deve ser rebocada por dois tratores A e B. Determine as intensidades das duas forças de reboque F A e F B , levando-se em conta que a força resultante tenha uma intensidade F R = 10 k N e
2.25. Duas forças F 1eF 2 atuem sobre o gancho. Se suas linhas de ação formam um ângulo θ e a intensidade de cada força é F 1 = F 2 = F , determine a intensidade da força resultante F R e o ângulo ent