Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 1.Problemas - Ex. 35

Demonstre que o volume comum aos cilindros de interseção definidos por x2 + y2 = a2 e x2 + z2 = a2 é V = 16a3/3.

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de matrizes, vetores e cálculo vetorial.

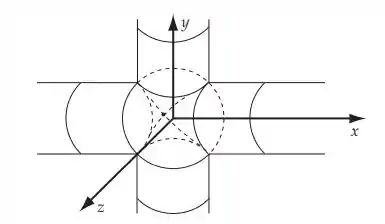
Calculamos o volume da interseção dos dois cilindros dividindo o volume da interseção em duas partes. Parte do volume comum é o de um dos cilindros, por exemplo, aquele ao longo do eixo y, entre y = –a e y = a:

V 1 = 2 π a 2 a = 2 π a 3

O restante do volume comum é formado por 8 partes iguais do outro cilindro (aquele ao longo do eixo x). Uma dessas partes se estende de x = 0 a x = a, y = 0 até y = a 2 - x 2 ,   z = a até z = = a 2 - x 2 . O volume complementar é então:

V 2 = 8 ∫ 0 a d x ∫ 0 a 2 - x 2 d y ∫ 0 a 2 - x 2 d z = 8 ∫ 0 a d x a 2 - x 2 a 2 - x 2 - a =

= 8 a 2 x - x 3 3 - a 2 2 s e n - 1 x a x = a - a 2 x - x 3 3 - a 3 2 s e n - 1 x a x = 0 =

= 8 a 3 - a 3 3 - a 3 2 π 2 = 16 3 a 3 - 2 π a 3

Somando os dois volumes temos que o volume total da interseção é:

V = V 1 + V 2 = 2 π a 3 + 16 3 a 3 - 2 π a 3 = 16 3 a 3

Resposta

Ver passo a passo.

Exercícios de Livros Relacionados

Demonstre quegrad (phi psi) = phi grad psi + psi grad phi
Demonstre queint ((overset(˙)(r))/(r) - (r overset(˙)(r))/(r^2)) d t = (r)/(r) + C onde C é um vetor constante.
Demonstre que:a ) underset(i , j)(sum) epsilon_i j k delta_i j = 0 b ) underset(j , k)(sum) epsilon_i j k epsilon_l j k = 2 delta_i l c ) underset(i j k)(sum) epsilon_i j k epsilon_i j k = 6
Utilize a notação epsilon_i j k e derive a identidade(A xx B) xx (C xx D) = (A B D) C - (A B C) D
Encontre o ângulo entre as superfícies definidas por r 2 = 9ex + y + z 2 = 1n op o n t o2 ,- 2 ,1 .