Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 111

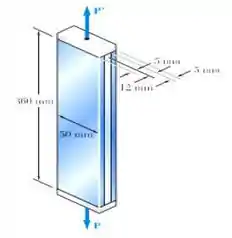
Duas barras de aço temperado, cada uma com espessura de 5 mm, são coladas a uma barra de aço doce de 12 mm. Essa barra composta é submetida a uma força axial centrada de intensidade P, conforme mostra a figura. Ambos os aços são elastoplástico com E = 200   G P a e com tensão de escoamento igual a 689,5   M P a   e   345   M P a , respectivamente, para o aço temperado e o aço doce. A força P é aumentada gradualmente desde zero até que a deformação da barra alcance um valor máximo de δ m = 1   m m e depois diminuída novamente até zero. Determine (a) o valor máximo de P, (b) a tensão máxima nas barras de aço temperado e (c) a deformação permanente depois de a força ser removida.

Passo 1

E ai pessoal tudo bem? Espero que sim !! o enunciado pede que a gente determine primeiramente a tensão máxima que ocorre no cabo BD. Antes vamos determinar a área vem comigo :D

Para o aço doce,

A 1 = 1 2   x   12 = 0,00064516   m 2

δ Y 1 = L σ Y 1 E = 0,05   x   ( 689,5   x   10 6 ) 2 00   x   10 6 = 0 , 172   m .

Para o aço temperado a mesma coisa gurizada :D

A 2 = 2   x   0,012   x   2 = 0 , 048   m 2           δ Y 2 = L σ Y 2 E = 0,05   x   345   x   10 6 200   x   10 6 = 0,08625 m

Área total: A = A 1 + A 2 = 0,258   m ²

Considerando:

δ Y 1 < δ m < δ Y 2

Agora partiu determinar os questionamentos do enunciado vem comigo :D

Passo 2

  1. Forças:

    2. P 1 = A 1 σ Y 1 = 0,258   x   689,5   x   10 6 = 17789   M P a P 2 = E A 2 δ m L = 2 0   x   10 6   x   0,258   x   0,08625 0,05 = 8,9   M P a

    A força total temos:

    P = P 1 + P 2 = 17789   M P a + 8,9   M P a = 1177979   M P a  

  2. Tensões: σ 1 = P 1 A 1 = σ Y 1 = 689,5   x   10 6 σ 2 = P 2 A 2 = 345   x   10 6 0,258 = 1337,2   M P a

    3. Deslocamento temos:

    δ ' = 0,000785876 .

  3. Para o total de deslocamento temos: δ p = 0,000230124   m

Resposta

  1. P = 1177979   M P a  
  2. 689,5   x   10 6 Pa
  3. 0,000230124   m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que P = 38 k N , determine a tensão máxima quando (a) r = 10 m , (b) r = 16 m m e (c) r = 18 m m .
Sabendo que o furo tem um diâmetro de 9,53 mm, determine (a) o raio r opara os quais ocorre a mesma tensão máxima no furo A e nos adoçamentos e (b) a força P correspondente máxima admissível se a tens
Sabendo que, para a placa mostrada, a tensão admissível é de 125 MPa. Determine o valor máximo admissível para P quando ar = 12m mebr = 18 m m .
Para P = 100k N , determine a espessura t mínima necessária para a placa se a tensão admissível for de 125M P a .
Uma força axial centrada e aplicada à barra de aço mostrada. Sabendo que σ m i n = 20k s i , determine a máxima carga P admissível.