Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 100 -

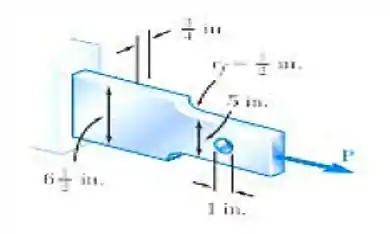
Uma força axial centrada e aplicada à barra de aço mostrada. Sabendo que σ m i n = 20   k s i , determine a máxima carga P admissível.

Passo 1

Fala aí gurizada tudo belezinha? O exercício pede que a gente determine a máxima carga P admissível, primeiramente vamos determinar no buraco do elemento, sendo o raio: r = 05   i n .                   d = 5 - 1 = 4   i n .

2 r d = 2   x   0,5 5 = 0,2                  

Agora temos que calcular a área deste orifício: A n e t = t d = 0,75   x   4 = 3   i n 2

Mas antes de encontrarmos a carga P gurizada, precisamos isolar ela da equação da tensão, então vem comigo :D

σ m a x = K P A n e t

P = A n e t σ m a x K = 3   x   ( 20 ) 2,51 = 23,9   k i p s

Passo 2

Agora precisamos determinar a carga no filete: temos que os diâmetros são:

D = 6,5   i n . ,               d = 5   i n . ,       D d = 6,5 5 = 1,3 n r = 0 , 5   i n .             r d = 0,5 5 = 0,1

Agora podemos determinar a área:

A m i n = t d = 0,75   x   5 = 3,75   i n 2

Considerando o valor de     K = 2,04 podemos determinar a carga P através da equação da tensão :D

σ m a x = K P A m i n P = A m i n σ m a x K = 3,75   x   ( 20 ) 2,04 = 36,8   k i p s

Resposta

P = 23,9   k i p s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra ABC consiste em duas porções cilíndricas AB e BC; ela é feita de um aço doce, que é assumido ser elastoplástico com E = 200 G P a e σ e = 250M P a . Uma força P é aplicada à barra até que sua
A barra de ligação horizontal BC é de 6,35 m m de espessura, tem uma largura w = 31,8m m e é feita de aço com tensão última de tração igual a 483M P a . Qual deve ser o coeficiente de segurança a ser
As barras AB e BE da treliça mostrada são da mesma liga metálica. Sabe-se que uma barra de 20 m m de diâmetro desta mesma liga foi testada até a falha e foi registrada uma carga máxima de 150k N . Usa
As barras AB e BE da treliça mostrada, são da mesma liga metálica. Sendo que a barra AB tem um diâmetro de 28 m m e que a carga máxima para a barra é de 300k N , determine:O coeficiente de segurança p
Para a emenda e carregamento do P r o b .1.36 , determine o coeficiente de segurança, sabendo-se que a resistência ultima da cola é de 1035k P a na tração e 1475k P a no cisalhamento.