Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 93

Sabendo que, para a placa mostrada, a tensão admissível é de 125 MPa. Determine o valor máximo admissível para P quando a   r = 12   m m   e   b   r = 18 m m .

Passo 1

Fala aí gurizada tudo belezinha ??? Determine o valor máximo admissível para P nos diferentes raios fornecidos no enunciado, então primeiramente vamos determinar a área do elemento, venham comigo !!!

A = 60   x   15 = 900   m m 2 = 900   x   10 - 6 m 2

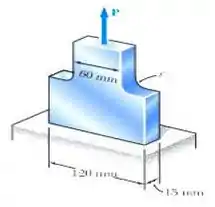
Notem na figura que temos 2 larguras, então vamos fazer a relação deste:

D d = 120   m m 60   m m 2,00

  1. Considerando o   r = 12   m m     ∴             r d = 12   m m 60   m m = 0,2       s e n d o   K = 1,92     , então temos que a tensão é determinada por:

    2.   σ m a x = K P A

    Isolando P temos: P = A σ m a x K = 900   x   10 - 6   x   125   x   10 6 1,92 = 58,6   x   10 3 N

  2. De maneira similar a opção A temos que considerar agora o   r = 18   m m ,     r d = 18   m m 60   m m = 0,30 sendo K = 1,75 P = A σ m a x K = 900   x   10 - 6   x   125   x   10 6 1,75 = 64,3   x   10 3 N

Resposta

a = 58,3   k N

b = 64,3   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A montagem mostrada consiste em um tubo de alumínio ( E = 70G P a ; α = 23,6 × 10 - 6 / ° C ) preenchido com núcleo de latão ( E = 105G P a ; α = 20,9 × 10 - 6 / ° C ) e, com ausência de tensão a uma
A montagem mostrada consiste em um tubo de alumínio ( E = 70G P a ; α = 23,6 × 10 - 6 / ° C ) preenchido com núcleo de aço ( E = 20 0G P a ; α = 11,7 × 10 - 6 / ° C ) e, com ausência de tensão a uma t
As hastes de ligação B C e D E são ambas de aço ( E = 200G P a ) e são de 1,25m m de largura por 6,35m m de espessura. Determinar: (a) a força em cada haste, quando uma força P de 2670N é aplicada à b
Uma barra composta de duas porções cilíndricas A B e B C é engastada em ambas as extremidades. A porção A B é de latão ( E = 105G P a ; α = 20,9 × 10 - 6 / ° C ) e a porção B C é de aço ( E = 200G P a
A barra rígida A B C D é suspensa por três cabos idênticos, como indicado. Sabendo-se que a = b , determinar a tração em cada cabo, causada pela carga P aplicada em C .