Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas Revisão - Ex. 182
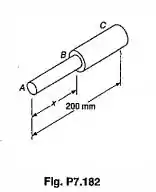
Duas barras de latão, AB, de de diâmetro e BC, de de diâmetro, serão soldadas juntas em B, para formar uma barra escalonada de comprimento total que irá ser engastada em C. Sabendo-se que a massa específica do latão é de determinar (a) o compartimento da barra ABpara que a tensão normal máxima em ABC seja mínima; (b) o correspondente valor da tensão normal máxima.
Passo 1
Fala aí galera do Responde aí, bora matar esse livro de resmat. Sabemos que o peso da barra irá exercer uma tensão normal nela. Devemos determinar esta tensão em função das variáveis dadas. O peso que a barra AB exerce será:
Já para a barra BC:
A tensão será dada pela força total sobre a área das barras:
Passo 2
Agora, vamos calcular a tensão total, que será a soma das tensões:
Como a função é linear, o menor valor para a tensão será o menor valor possível de que no caso é 0. Logo:
Passo 3
Agora, basta calcular a tensão com o valor de Refazendo: