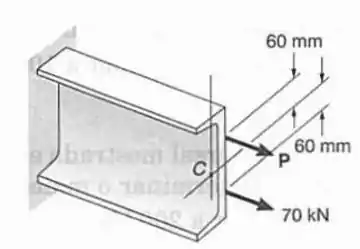
Duas cargas horizontais são aplicadas como mostrado a um curto perfil laminado de aço . Sabendo-se que a tensão de tração neste perfil não deve exceder a , determinar a maior carga permissível.
Passo 1
A tensão no ponto será igual a:
Logo, para resolver este problema basta achar a área, os momentos decompostos em e , assim como os momentos de inércia também decompostos. Vamos lá!?
Passo 2
O problema já traz o fato de ser um perfil que tem as seguintes características:
Passo 3
A força vai gerar um momento em da mesma forma que a força de mas cada uma num sentido diferente, então:
Além disso, como as forças e a de não está alinhada no centro da peça irá gerar um momento também no eixo :
Passo 4
Agora é só substituir na equação:
Vamos utilizar como metade do comprimento da aba do nosso perfil e no lugar de vamos utilizar a altura da aba