Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 120

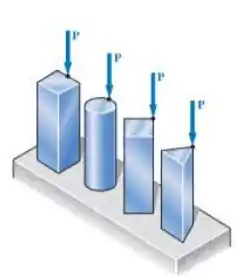
As quatro barras mostradas na figura têm a mesma área de seção transversal. Para os carregamentos dados, mostre que:

  1. As tensões de compressão máxima estão na relação 4:5:7:9 e
  2. As tensões de tração máximas estão na relação 2:3:5:3.

(sugestão: a seção transversal de uma barra triangular é um triangulo equilátero)

Passo 1

Fala galera, aqui vamos ter que analisar cada uma das seções separadamente, e você vai ver que vai ser bem tranquilo. Mas antes de tudo, vamos dar uma mexida no nosso cálculo de tensão, sabemos que o calculo da tensão de compressão é dado por:

σ c o m p r e s s ã o = - P A - M y c o m p r e s s ã o I

E como a nossa carga está deslocada com relação ao centroide, e consequentemente, com relação a LN, teremos que o nosso momento pode ser escruto como a carga multiplicada por uma excentricidade, assim teremos que:

σ c o m p r e s s ã o = - P A - P e y c o m p r e s s ã o I = - P A 1 + A e y c o m p r e s s ã o I

E usando o mesmo princípio para a tração, teremos que:

σ t r a ç ã o = - P A - M y t r a ç ã o I

σ t r a ç ã o = - P A - P e y t r a ç ã o I = P A A e y t r a ç ã o I - 1

Assim, sabendo a maneira que iremos calcular a tensão nas nossas seções, podemos analisar cada uma delas separadamente.

Passo 2

A nossa seção 1 é quadrada, ou seja, podemos considerar ela com lados iguais, assim, as dimensões da nossa seção, são dadas aqui embaixo:

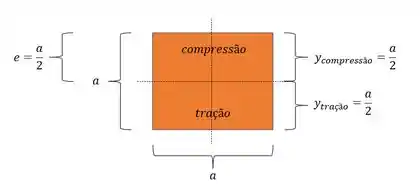
Assim temos que:

A = a 2

I = a a 3 12 = a 4 12

y c o m p r e s s ã o = a 2

y t r a ç ã o = a 2

e = a 2

Substituindo temos que:

σ c o m p r e s s ã o = - P A 1 + a 2 a 2 a 2   a 4 12 = - P A 1 + 12 4 = - 4 P A

σ t r a ç ã o = P A a 2 a 2 a 2 a 4 12 - 1 = P A 12 4 - 1 = 2 P A

Vamos agora para a seção circular.

Passo 3

A nossa seção 2 é circular, ou seja, podemos considerar ela com um raio r, assim, as dimensões da nossa seção, são dadas aqui embaixo:

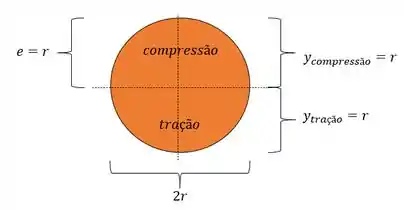
Assim temos que:

A = π r 2

I = π r 4 4

y c o m p r e s s ã o = r

y t r a ç ã o = r

e = r

Substituindo temos que:

σ c o m p r e s s ã o = - P A 1 + π r 2 r r   π r 4 4 = - P A 1 + 4 = - 5 P A

σ t r a ç ã o = P A π r 2 r r   π r 4 4 - 1 = P A 4 - 1 = 3 P A

Vamos agora para a seção quadrada girada.

Passo 4

A nossa seção 3 é quadrada e girada , ou seja, podemos considerar ela com algumas diferenças importantes, assim, as dimensões da nossa seção, são dadas aqui embaixo:

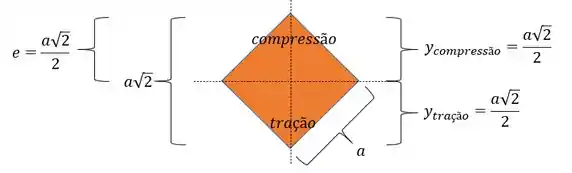
Assim temos que:

A = a 2

O momento de inércia de seções quadradas tem algo interessante que podemos notar, a inércia dela girada, e a inércia horizontal são iguais, assim temos que:

I = a a 3 12 = a 4 12

Quanto as outras tensões temos que:

y c o m p r e s s ã o = a 2 2

y t r a ç ã o = a 2 2

e = a 2 2

Substituindo temos que:

σ c o m p r e s s ã o = - P A 1 + a 2 a 2 2 a 2 2   a 4 12 = - P A 1 + 6 = - 7 P A

σ t r a ç ã o = P A a 2 a 2 2 a 2 2   a 4 12 - 1 = P A 4 - 1 = 5 P A

Vamos agora para a seção triangular.

Passo 5

A nossa seção 4 é triangular, ou seja, podemos considerar ela com algumas diferenças importantes, assim, as dimensões da nossa seção, são dadas aqui embaixo:

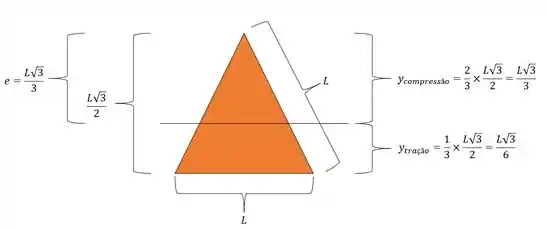
Assim temos que:

A = L × L 3 2 × 1 2 = L 2 3 4

I = b h 3 36 = L L 3 2 3 36 = L 4 3 3 8 × 36 = 3 L 4 9 6

y c o m p r e s s ã o = L 3 3

y t r a ç ã o = L 3 6

e = L 3 3

Substituindo temos que:

σ c o m p r e s s ã o = - P A 1 + L 2 3 4 L 3 3 L 3 3   3 L 4 96 = - P A 1 + 8 = - 9 P A

σ t r a ç ã o = P A L 2 3 4 L 3 3 L 3 6   3 L 4 96 - 1 = P A 4 - 1 = 3 P A

Agrupando todas as tensões, e sabendo que como o enunciado disse, todas possuem a mesma área, obtemos o seguinte:

  • Compressão

    • - 4 P A : - 5 P A : - 7 P A : - 9 P A

    Retirando tudo que é comum, teremos que:

    4 : 5 : 7 : 9

  • Tração

    • 2 P A : 3 P A : 5 P A : 3 P A

    Retirando tudo que é comum, teremos que:

    2 : 3 : 5 : 3

    Resposta

  • Compressão

    • - 4 P A : - 5 P A : - 7 P A : - 9 P A

    Retirando tudo que é comum, teremos que:

    4 : 5 : 7 : 9

  • Tração

2 P A : 3 P A : 5 P A : 3 P A

Retirando tudo que é comum, teremos que:

2 : 3 : 5 : 3

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o componente de máquina e o carregamento indicado, determinar as tensões nos pontos A e B , quando h = 60m m .
Para a barra curva e o carregamento mostrado, determinar a máxima tensão de compressão quando: (a) r = 45m m ;
Para a barra curva e o carregamento mostrado, determinar a tensão nos pontos A e B , quando: r 1 = 8m m
A seção Z mostrada está sujeita a um momento M 0 , atuando em um plano vertical. Determinar o maior valor permissível do momento fletor M 0 , se a máxima tensão não excede 100M P a . Dados: I m á x =
Uma viga com a seção transversal mostrada está submetida a um momento M 0 , que atua em um plano vertical. Determinar o maior valor permissível do momento fletor M 0 , se a máxima tensão na viga não e