Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 126
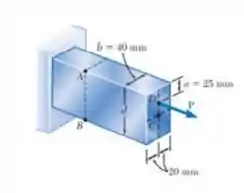
A força axial excêntrica P atua no ponto D, que deve estar localizada abaixo da superfície superior da barra de aço mostrada. Para , determine.
- A altura da barra para a qual a tensão de tração no ponto é máxima e.
- A tensão correspondente no ponto A.
Passo 1
Para podermos determinar a largura da barra afim de termos a tensão do ponto A máxima, precisamos definir a tensão na barra em função do que temos, sendo assim, temos que lembrar que a tensão na barra tem que ser definida da seguinte maneira.
Sabemos que:
Em que é a excentricidade da carga com relação ao centroide da seção. Com isso temos que:
Sabemos também que:
Substituindo teremos que:
Passo 2
Como queremos o valor de que produz a máxima tensão de tração, precisamos derivar a nossa equação anterior, e igualar ela a zero, pois assim obtemos exatamente a máxima tração atuante na nossa seção, assim, temos que:
Assim isolando, temos que:
Ou seja, temos que a máxima altura é dada por:
E assim, pelo enunciado temos que , assim temos que:
E assim resolvemos o item a).
Passo 3
Sabemos que a fórmula de tensão é dada por:
E queremos a máxima tensão usando a altura que descobrimos no item a), assim temos que os dados são:
Substituindo, temos que: