Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas de Revisão - Ex. 159
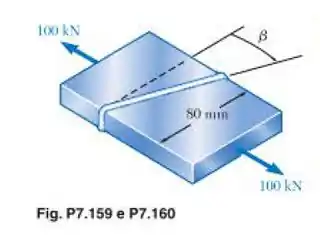
Duas chapas de aço de seção transversal uniforme de 10 x 80 mm são soldadas juntas conforme mostrado. Sabendo que forças de 100 kN são aplicadas às placas soldadas e que , determine (a) a tensão de cisalhamento no plano paralela à solda, (b) a tensão normal perpendicular à solda.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos precisar encontrar as forças normal e tangente à solda, para que então possamos encontrar a tensão tangencial (de cisalhamento) e a tensão normal a ela. Para isso, vamos desenhar um DCL para o sistema para nos auxiliar a determinar essas forças, então bora lá!
Passo 2
Beleza! Vamos começar desenhando o DCL para a região da solda, onde teremos:
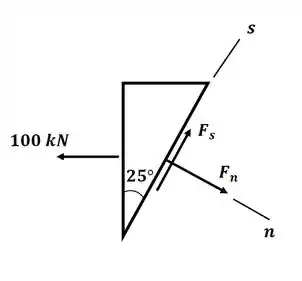
Então agora, vamos aplicar o somatório de forças na direção s, obtendo:
Agora, da mesma forma, vamos aplicar o somatório de forças na direção n, onde teremos:
Agora, com as forças nas direções normal e tangencial encontradas, podemos resolver a letra (a), que nos pede a tensão de cisalhamento paralela a solda, ela será dada por:
Em que é a área da solda, que precisamos calcular. Ela será dada por:
Então a tensão de cisalhamento será:
Agora vamos pra letra (b).
Passo 3
Agora para a letra (b), vamos encontrar a tensão perpendicular a solda, ou seja, a tensão normal, que será dada por:
Aqui é só a gente substituir os valores conhecidos, chegando em:
Shooow! Terminamos mais um, valeeu!