Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 20
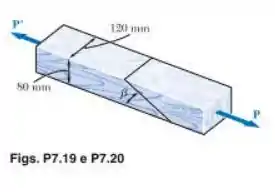
Dois elementos de madeira de seção transversal retangular uniforme de são unidos por uma junta colada conforme mostra a figura. Sabendo que e que as tensões máximas admissíveis na junta são, respectivamente, em tração e em cisalhamento, determine a maior força centrada que pode ser aplicada.
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Bora pra outra questão.
Como a tensão é a força sobre a área, precisamos calcular a área da seção inclinada. A área será:
Neste caso, as direções serão paralelas ou perpendiculares à seção.
A tensão de resistência a tração é igual a força normal máxima sobre a área
Sendo que a força normal é a força P decomposta na direção perpendicular à seção:
Logo,
Passo 2
A tensão de resistência ao cisalhamento é igual a força de cisalhamento máxima sobre a área
Sendo que a força normal é a força P decomposta na direção perpendicular à seção:
Logo,
Para determinar o valor máximo da carga P, temos que olhar pro menor valor encontrado, pois a tensão não pode ultrapassar os limites de tração nem de cisalhamento.