Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 39

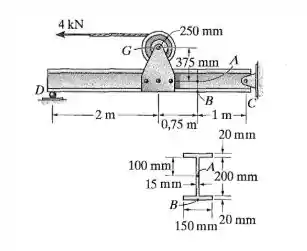
Determine o estado de tensão no ponto A quando a viga está sujeita à força de 4 kN no cabo. Indique o resultado como um elemento de volume diferencial.

Passo 1

Fala aí galera, partiu mais um problema de resmat pra gente ficar craque na matéria. O primeiro passo do problema é calcular as reações de apoio, logo:

C x = 4 k N

∑ M d = 0 → C y = 0,667 k N

D y = - 0,667 k N

Com isso, basta determinar os esforços atuantes em A:

N = 4 k N

V = 0,667 k N

M = 0,667 × 1 = 0,667 k N m

Agora, precisamos calcular o momento de inércia e o momento estático da seção transversal:

I = 2 0,15 × 0,02 3 12 + 0,15 × 0,02 × 0,11 2 + 0,015 × 0,2 3 12 = 8,28 × 10 - 5 m 4

Q = 0,05 × 0,1 × 0,015 + 0,11 × , 15 × 0,02 = 4,05 × 10 - 4 m ³

Passo 2

Com isso, basta calcular as tensões pedidas:

σ = N A + M y I

τ = V Q I t

Substituindo os valores, ficaremos com:

σ = 0,444 M P a

τ = 0,217 M P a

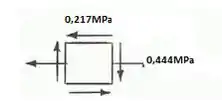
Esboçando o elemento, teremos:

Resposta

σ = 0,444 M P a

τ = 0,217 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

P 1 e P 2 são aplicadas, como mostrado na figura, em direções perpendiculares ao eixo longitudinal de uma viga W310x60. Sabendo que P 1 = 25 k N e P 2 = 24 k N , determine as tenções principais e a te
Desprezando o efeito dos adoçamentos e das concentrações de tensões, determine os menores diâmetros permissíveis para as hastes sólidas BC e CD. Utilize T a d m = 60 M P a .
a) Sabendo que σ a d m = 165,5 M P aeτ a d m = 100 M P a , selecione o perfil de mesa larga mais econômico que deverá ser utilizado para suportar o carregamento mostrado. (b) Determine os valores a se
b.
a) no ponto a e b no ponto b