Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 63
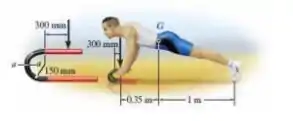
O homem tem massa de 100 kg e centro de massa em G. Se ele mantiver na posição mostrada na figura, determine a tensão de tração máxima e a tensão de compressão máxima desenvolvida na seção a-a da barra curva. Ele é suportado uniformemente pelas duas barras, e cada uma delas tem diâmetro de 25 mm. Considere que o piso é liso.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora.
Bom, nosso enunciado nos diz que esse carinha que mora logo ali e resolveu fazer barra, e nos pede a tração e a compressão máxima.
Mas vamos entender o que está acontecendo ali. O homem, a gente pode encarar como uma viga biapoiada. Porque ele apoia no chão pelos pés e nas duas barras (igualmente) com as mãos. E em temos o peso dele.
E numa barra, a gente tem esse efeito da reação de apoio do homem. Temos algo assim:
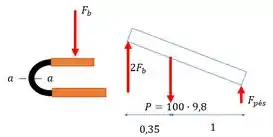
Repara que o homem é suportado por duas barras, por isso . Precisamos achar os esforços em . Bora!
Passo 2
Nosso primeiro passo será calcular . Pois essa força atua barra, e como sabemos que vale:
Podemos determinar através do somatório dos momentos, tal que:
Portanto, a soma das forças em nos fornece que:
Passo 3
Pronto!! Com as nossas forças externas calculadas, vamos achar as nossas forças internas em , ou seja, a normal e os momentos, porque só esses esforços geram força normal.
A gente vai cortar nossa seção em . Olha só para parte de cima, ode a gente conhece a força aplicada. Posicionamos os esforços internos na seção e achamos pelas equações de equilíbrio
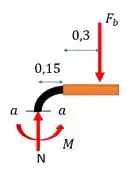
Então para as forças em :
E para os momentos, obtemos:
Passo 4
Agora que já temos todo o necessário para calcular nossas tensões, por que vamos esperar?? Só bora comigo.
Mas antes, algo importante: a gente tem uma barra curva. Nela, a distribuição de tensão não é linear. Ela vai seguir essa fórmulinha:
Como nossa seção é circular, esse vai ser dado pela fórmula:
é o raio da seção transversal e é a distância do centro de curvatura até onde a tensão é determinada.
Agora vamos trazer uns dados muuuuuito importantes pra nos ajudar com as contas.
Nosso é a distância do centro do nosso raio da barra até a parte do ponto a do corte mais distante, ou seja, o raio da curvatura da barra mais o diâmetro da seção.
Ele vai ser o para a tensão de tração.
O nosso ri é a distância do nosso centro de curvatura da barra mais a distância até o ponto a do corte mais perto, ou seja, é só o raio mesmo.
Ele vai ser o para a compressão.
E o nosso r’ é o raio médio entre esses dois aí, que a gente pode calcular como sendo o raio da curvatura mais o raio da barra.
Calculando :
Sendo assim:
Passo 5
Aí nossas tensões ficam, primeiro :
E para , obtemos que: