Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 22

As duas esferas estão rigidamente conectadas à haste de massa desprezível e estão inicialmente em repouso sobre a superfície horizontal lisa. Uma força F é aplicada repentinamente a uma esfera na direção y e transmite um impulso de 10   N ∙ s durante um período desprezivelmente curto de tempo. Quando as esferas passam pela posição tracejada, calcule a velocidade de cada uma.

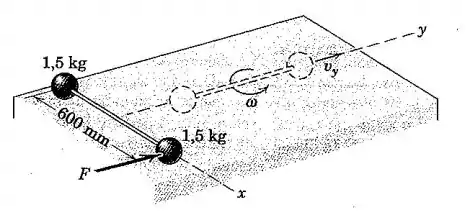
Passo 1

Lembre-se que o impulso de uma força é igual à variação da quantidade de movimento. Então, para a direção x , temos:

Δ G x = I x = ∫ ∑ F x d t = 0

E para a direção y :

Δ G y = I y

1,5 v y + 1,5 v y = 10

v y = 3,33   m / s

Passo 2

Nós não conseguimos calcular v x por meio do impulso porque as velocidades em x de cada esfera têm igual módulo e sentidos opostos, devido à conservação da quantidade de movimento na direção x .

Porém, podemos usar a equação da quantidade de movimento angular para o centro de massa:

Δ H G = ∫ ∑ M G d t

2 m v x r = I r

2 1,5 v x 0,600 2 = 10 0,600 2

v x = 3,33   m / s

Então, a velocidade das duas esferas será:

v = 3,33 2 + 3,33 2

v = 4,71   m / s

Resposta

v = 4,71   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 13.136, considerando que o peso do bloco é 17,84 kg.
Um bloco de 12,74 kg em repouso é acionado por uma força P que varia como mostrado na figura. Sabendo que os coeficientes de atrito entre o bloco e a superfície são μ s = 0,50, μ k = 0,40 determine (a
Um transatlântico de 40M g toneladas tinha sua velocidade inicial de 4k m / h . Desprezando a resistência ao atrito da água, determine o tempo necessário para trazer o transatlântico para o repouso us
Uma mãe e seu filho estão esquiando juntos, com a mãe segurando a ponta de uma corda amarrada na cintura do filho. Eles estão se movendo a uma velocidade de 7,2k m / h na parte plana de uma trilha de
Dois blocos A e B estão conectados por uma corda que passa pelas roldanas e por meio de um colar C . O sistema é liberado do repouso quando x = 1,7m . Como o bloco A sobe, ele bate no colar C com impa