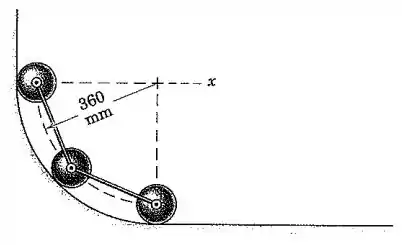
As três pequenas esferas de aço, cada uma com massa de , estão unidas pelas conexões articuladas de massa desprezível e comprimentos iguais. As esferas são liberadas a partir do repouso nas posições mostradas e deslizam para baixo a guia de um quarto de círculo no plano vertical. Quando a esfera de cima atinge a posição na base, as esferas possuem uma velocidade horizontal de . Calcule a perda de energia devida ao atrito e o impulso total sobre o sistema de três esferas durante esse intervalo.

Para o cálculo da variação da energia potencial gravitacional, consideramos a altura final (nível do chão) como zero, e então será dada em função das alturas iniciais , e das esferas contadas a partir da esquerda para a direita:

Porém, pela geometria da figura, temos:

Então:

Logo:

Para calcular o impulso em , basta lembrar que ele é igual à variação da quantidade de movimento em :

Como as esferas foram liberadas a partir do repouso, temos :