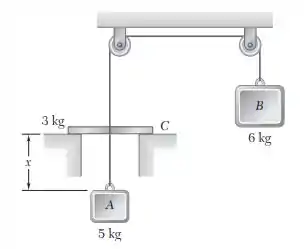
Dois blocos e estão conectados por uma corda que passa pelas roldanas e por meio de um colar . O sistema é liberado do repouso quando . Como o bloco sobe, ele bate no colar com impacto plástico perfeito . Após o impacto, os dois blocos e o colar se mantêm movendo até que param e revertem seus movimentos. Como e se movem para baixo, atinge o ressalto e os blocos e se mantêm em movimento até que param novamente. Determine a velocidade dos blocos e do colar imediatamente após A atingir , a distância que os blocos e colar se movem após o impacto antes de parar, o valor de no final de um ciclo completo.

Fala aí, galerinha. Tudo certo? Bora para mais uma questãozinha de Dinâmica. Primeiro, vamos determinar a velocidade antes do impacto. Por conservação de energia, no instante inicial, temos:

E em um segundo instante, temos:

Logo, a energia cinética vai ser:

Vamos esboçar o problema para entendermos melhor o que está acontecendo. Fica assim:

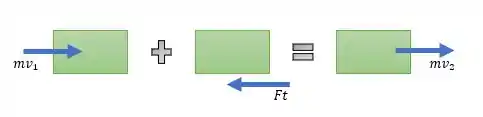
Este diagrama representa as quantidades de movimento em dois instantes, e , e o impulso da força exercida pelo rebocador para que o transatlântico fique em repouso, ou seja, .

Com isso, podemos determinar o tempo necessário para que o transatlântico entre em repouso a partir do princípio de impulso e quantidade de movimento. Sabemos que ele é dado por:

Substituindo:

Convertendo as unidades, temos:

É isso, galerinha. Bora praticar mais pra ficar craque!