Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 136

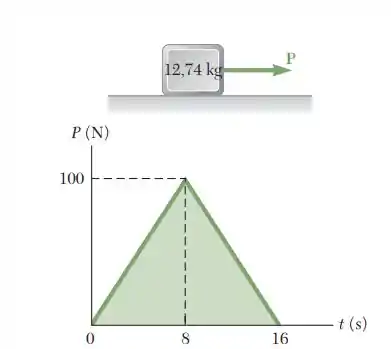
Um bloco de 12,74 kg em repouso é acionado por uma força P que varia como mostrado na figura. Sabendo que os coeficientes de atrito entre o bloco e a superfície são μ s = 0,50, μ k = 0,40 determine (a) o tempo no qual o bloco começará a se mover, (b) a velocidade máxima alcançada do bloco, (c) o tempo no qual o bloco vai parar de se mover.

Passo 1

Vamos lá resolver mais essa. Para determinar o tempo que o bloco começará a se mover, vamos utilizar o princípio de impulso e quantidade de movimento. Observando a figura abaixo:

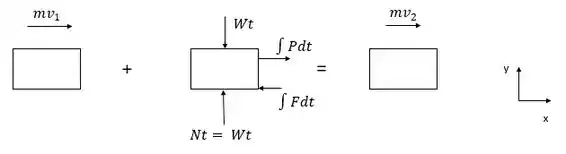
Temos que:

m v 1 + ∫ P d t - ∫ F d t = m v 2

v = 1 m ∫ P d t - ∫ F d t

Essa é a velocidade do bloco para qualquer instante de tempo. O bloco irá se mover quando P = F = F a t . Observando o gráfico

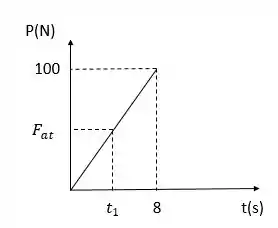
Podemos, por semelhança de triângulos, determinar o instante que o bloco começará seu mevimento:

t 1 8 = F a t 100 → F a t = μ s N =   μ s m g = 0,50 ⋅ 12,74 ⋅ 9,81 = 62 , 5   N

t 1 = 8 62 , 5 100 = 5 , 0   s

Passo 2

Após o bloco iniciar seu movimento, ele atingirá a velocidade máxima quando sua aceleração for igual a zero, ou seja, quando P = F a t , sendo essa a força de atrito cinético. Definindo este instante com t m , temos que:

P = F a t = μ k m g = 0,40 ⋅ 12,74 ⋅ 9,81 = 5 0,0   N

Assim, colocando as informações do passo anterior e deste passo no gráfico, conforme a figura abaixo:

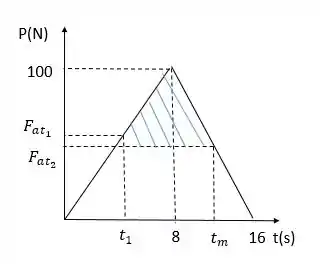
Temos que o impulso máximo, que irá fornecer a velocidade máxima ao bloco, é igual a área da parte hachurada. Para descobrirmos t m , vamos fazer da mesma forma para t 1 :

16 - t m 8 = F a t 2 100 → t m = 16 - 8 5 0 100 = 12   s

Assim:

v m = 1 m 1 2 12,5 + 5 0 3 + 1 2 5 0 12 - 8

v m = 1 12,7 4 ( 193,75 )

v m = 15,2   m / s

Passo 3

O bloco para de se mover quando o impulso líquido é igual a zero, ou seja:

∫ ( P - F ) d t = 0

Para isso, vamos assumir um tempo t f < 16   s , em que t f é o instante que o bloco para de se mover. Observando o gráfico de impulso (P –F) x t:

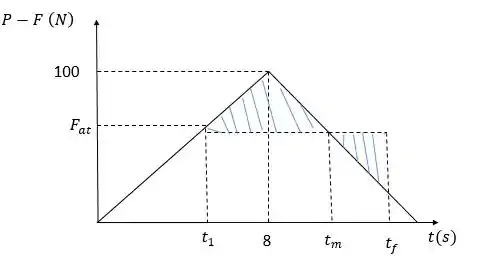
É uma subtração das áreas dos gráficos P x t e F x t:

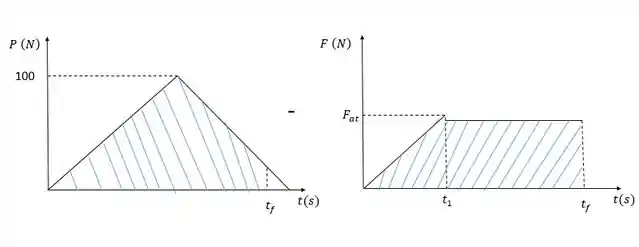
Assim, para calcular t f , vamos fazer a subtração da área hachurada do gráfico da esquerda pela a área hachurada do gráfico da direita. O valor de P quando t = t f pode ser obtido por meio da semelhança de triângulos:

16 - t f 8 = P f 100 → P f = 100 16 - t f 8

Calculando a área de cada gráfico:

∫ 0 t s P d t = 1 2 100 8 + 1 2 100 + 100 16 - t f 8 t f - 8 = 800 - 6,25 16 - t f 2

∫ 0 t f F d t = 1 2 62 , 5 5 + 50 t f - 5 = 156,25 - 5 0 ( t f - 5 )

∫ P d t - ∫ F d t = 800 - 6,25 16 - t f 2 - 156,25 - 50 t f - 5 = 0

t f = 17,6   s

Resposta

  1. 5,0 s
  2. 15,2 m/s
  3. 17,6 s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O seguinte modelo matemático foi sugerido para a variação na pressão dentro do diâmetro de 10 mm do cano de um rifle quando uma bala de 25 g é disparada: p t = 950M P a e - t / ( 0,16m s ) onde t é ex
Uma estimativa da carga esperada sobre cintos de segurança é feita antes de se desenhar protótipos de cintos que serão avaliados em testes de impacto com automóveis. Admitindo que um automóvel que rod
Um modelo simplificado baseado em uma linha reta deve ser obtido para a variação de pressão dentro do cano de um rifle de 10 mm de diâmetro durante o disparo de uma bala de 20 g. Sabendo que leva 1,6
Uma força constante P é aplicada a um pistão e haste de massa total m para fazê-los se mover em um cilindro cheio de óleo. Conforme o pistão se move, o óleo é forçado através dos orifícios no pistão e
A mola AB de k constante é fixada a um suporte em A e a um colar de massa m. O comprimento não alongado da mola é l . Sabendo que o colar é liberado do repouso em x = x 0 e desprezando o atrito entre