Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 24b

Duas forças são aplicadas como mostrado na barra AB, que é soldada ao cilindro DE, de diâmetro 50mm. Considerando que todas as tensões permanecem abaixo do limite de proporcionalidade, determinar as tensões principais e a máxima tensão de cisalhamento no:(a) ponto H; (b) ponto K.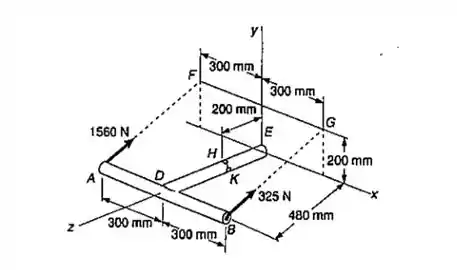

Passo 1

Fala aí, bora resolver esse item b?

Vamos começar decompondo as forças no ponto A e B, nas direções y e z.

B G = 480 2 + 2 00 2 = 5 20 m m

F y 1 = 200 520 × 325 = 125 N

F y 2 = 200 520 × 1560 = 600 N

F z 1 = - 480 5 20 × 325 = - 300 N

F z 2 = - 48 0 5 20 × 1560 = - 1440 N

Passo 2

Beleza, agora vamos analisar os esforços na seção. As forças em Z causam momento em y como mostrado no esquema:

M y = + 300 × - 300 - 300 × - 1440 = 342 × 10 3 N . m m

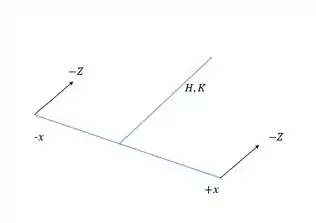
Pela regra da mão direita a gente observa que o sentido de M y é negativo.

M y = 342 × 10 3 N . m m ( - y ^ )

Essas forças também serão somadas e causarão tensões normais no ponto K e H:

N z = F z 1 + F z 2 = - 1 740 N

As forças em y, vão causar cisalhamento e dois tipos de momento na seção:

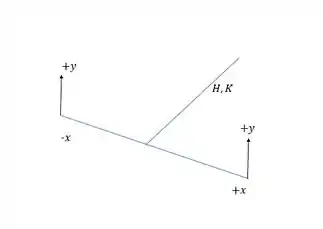
O esforço cortante na seção será:

V = F y 1 + F y 2 = 725 N

Com o desenho fica mais fácil da gente ver os efeitos, em torno do eixo Z teremos momento torsor e em torno de X momento fletor.

T = 300 × 125 - 300 × 600 = - 142,5 × 10 3 N . m m

M x = 125 + 600 × 480 - 200 = 203 × 10 3 N . m m ( -   x ^ )

Show de bola, temos agora todos os esforços atuantes na seção.

Passo 3

Vamos calcular as propriedades geométricas:

A = π d 2 4 = 1 9 63,5 m m ²

J = π r 4 2 = 613,59 × 10 3 m m 4

I = J 2 = 306,8 × 10 3 m m 4

E o momento estático de um semicírculo:

Q = 2 3 r 3 = 10,41 × 10 3 m m 3

t = d = 50 m m

c = r = 25 m m

Passo 4

Vamos analisar o que acontece pro ponto K, localizado no centro da seção.

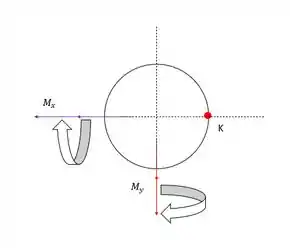
A influência do momento fletor é a que geralmente mais confunde nossa cabeça, mas repara o seguinte, somente o momento em Y vai causar tensões no ponto K, pois a linha neutra do momento em X passa por K.

Usando a regra da mão direita a gente pode ver que o efeito em K do momento em Y é de tração(+).

σ x 1 = M y c I = 342 × 10 3 × 25 306,8 × 10 3 = + 27,87 M P a

A outra influência de compressão será:

σ x 2 = N A = - 1740 N 1863,5 = - 0 , 934 M P a

σ x = σ x 1 + σ x 2 = + 26,936 M P a

A influência do torsor na seção é dada por:

τ 1 = T c J = - 1 42,25 × 10 3 × 25 613,59 × 10 3 = - 5,8 M P a

No caso do ponto K, há influência do momento estático no cisalhamento. A tensão cisalhante no centro é:

τ 2 = V Q I t

τ 2 = 725 × 10,41 × 10 3 50 × 306,8 × 10 3 = + 0,492 M P a  

τ = τ 1 + τ 2 = 5,31 M P a

Passo 5

Vamos colocar esses valores no círculo de Mohr e ver o que a gente consegue tirar.

σ x = + 26,936 M P a

σ y = 0

τ x y = - 5 , 31 M P a

E com isso:42

c = ( σ x + σ y ) 2 = + 13,47 M P a

Lembrando que:

τ m á x = R = σ x - c 2 + τ x y 2 = 1 4,48 M P a  

E enfim:

σ 1 = c + r = 28 M P a

σ 2 = c - r = - 1,01 M P a

Resposta

σ 1 = 28 M P a

σ 2 = - 1 , 01 M P a

τ m á x = 14,48 M P a  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar a carga uniformemente distribuída admissível w , para a viga mostrada, sabendo-se que σ a d m = + 70M P a na tração, σ a d m = - 130M P a , na compressão, e que τ a d m = 60M P a .
Uma barra de aço uniforme de diâmetro d é içada por cabos de um guindaste, amarrados em A e B . Pede-se: (a) determinar a distância a , entre as extremidades da barra e os pontos onde os cabos estão a
Sabendo-se que τ a d m = 50M P a , determinar o menor diâmetro permissível para o eixo maciço A B , quando P = 2N , l = 30 0m m e L = 75m m . Incluir o efeito das tensões de cisalhamento, causadas pel
Usando a notação da Sec. 7.9 e desprezando o efeito das tensões de cisalhamento, causadas por cargas transversais; mostrar que a máxima tensão normal, em um eixo circular, pode ser expresso como segue
Para o eixo A B e a alavanca A C , mostrar que o efeito das tensões de cisalhamento, causadas pela carga transversal, devem ser incluídas para que se obtenha o valor exato da máxima tensão. L d1 3 1 +