Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 95

Resolver o Prob. 6.94, considerando que o sentido da força P é o inverso.

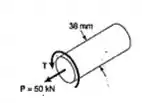
Passo 1

Fala aí, vem comigo matar essa questão de critérios de falha?

Vamos começar analisando o que a gente tem e reunindo as equações que vamos precisar:

Temos um esforço de torção que causa tensão cisalhante, e um esforço normal de tração que vai causar tensão normal.

σ x = P A

τ = T c J

Passo 2

Bom, agora bora calcular as propriedades geométricas da nossa peça pois serão necessárias pro cálculo das tensões.

A = π d 2 4 = 1017,87 m m ²

c = r = 36 2 = 18 m m

J = π r 4 2 = 164,9 × 10 3 m m 4

Passo 3

Agora voltamos nas equações de tensão e substituindo:

σ x = - 50 × 10 3 1017,87 = - 49,122 M P a

Enquanto não temos o valor de T, vamos manter a tensão cisalhante dessa forma o que vai economizar algumas contas pra gente.

τ = T c J

Se liga aqui! Precisamos encontrar os planos principais pra gente trabalhar com o nosso critério.

c = σ x + σ y 2 = - 24,561 M P a

Como só temos σ x :

r = σ x 2 2 + τ ²

E as tensões principais são.

σ 1 = c + r

σ 2 = c - r

Passo 4

Agora vamos aplicar o critério de Mohr, que diz que pro material falhar deve ser atingido o valor abaixo:

σ 1 σ u t - σ 2 σ u c = 1

1 40 σ 1 - 70 σ 2 = 70 × 1 4 0

1 40 c + r - 70 c - r = 70 × 1 4 0

Dividindo toda essa galera por 70temos:

2 c + r - c - r = 140

3 r - c = 140

3 r = 120 - 24,561

r = 31,813 M P a

Passo 5

Show de bola, agora é só a gente lembrar que:

r = σ x 2 2 + τ ²

Rearrumando:

τ = r 2 - 24,561 2

Substituindo r= 31,813.

τ = 20,22 M P a

E enfim:

T = τ J c

T = 20,22 × 164,9 × 10 3 18 = 185,24 × 10 3 N . m m

T = 185,24 N . m

Resposta

T = 185,24 N . m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo de alumínio com 250 mm de comprimento (E = 70G P a ) , 36 mm de diâmetro externo de 28 mm de diâmetro interno pode ser fechado em ambas as extremidades por meio de tampas com rosca simples de
Ambas as partes da barra ABC são feitas de um alumínio para o qual E = 70G P a . Sabendo que a intensidade de P é 4 kN, determine (a) o valor de Q e modo que o deslocamento em A seja zero e (b) o desl
O comprimento do fio de aço CD de 3 32 in diâmetro foi ajustado de modo que, sem nenhuma força aplicada, existe um espaço de 1 16 i n entre a extremidade B da barra rígida ACB e um ponto de contato E.
Os elementos AB e BC são feitos de aço (E = 29x10 6 p s i ) e têm seção transversal com área de 0,80i n 2e0,64i n 2 , respectivamente. Para o carregamento mostrado, determine o alongamento do (a) elem
Cada uma das barras AB e CD é feita de alumínio ( E = 10,9x10 6 p s i e tem uma seção transversal com área de 0,2 i n 2 . Sabendo que elas suportam a barra rígida BC, determine o deslocamento do ponto