Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 116
Determinar a carga uniformemente distribuída admissível , para a viga mostrada, sabendo-se que na tração, , na compressão, e que .
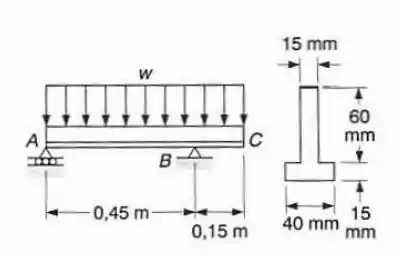
Passo 1
Oi, fala aí, galerinha!!! Para resolver esse problema a gente vai seguir o seguinte passo a passo:
- Calcular o módulo resistente da seção .
- Calcular a força cortante, o momento fletor e achar o momento fletor máximo em função de .
- O momento fletor calculado pode ser utilizado para calcular novamente o módulo resistente, dessa forma, vamos comparar os dois e assim poderemos achar o valor máximo de
Então partiu pro exercício!
Passo 2
Vamos calcular o módulo resistente da seção:
Onde é o momento de inércia e maior distância entre a linha neutra e a superfície da peça. Vamos calcular o momento de inércia então, mas primeiro precisamos achar a linha neutra:
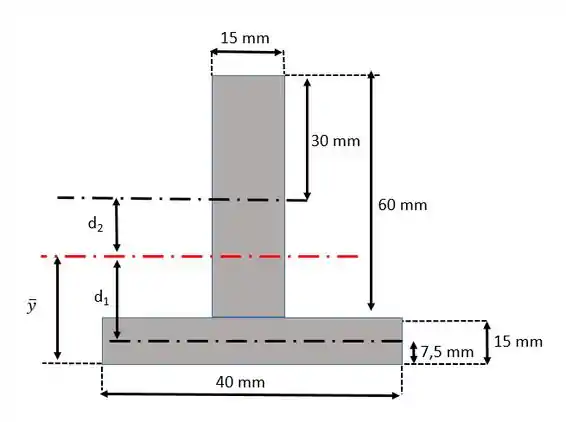
Temos duas áreas, cada uma representando um retângulo então vamos ter:
Logo a posição da linha neutra será em:
Passo 3
Show! Agora podemos achar o momento de inércia, utilizando a equação do momento de inércia para uma barra retangular e o teorema dos eixos paralelos:
Onde é a distância entre o centroide da figura e a linha neutra.
Calculando:
Agora para a segunda barra (vertical)
Agora é só somar:
Passo 4
Quase lá, galera!!! Falta só aplicar a distância :
Como o problema diferencia a carga admissível para a tração a para a compressão a gente tem que fazer esta distinção aqui também, issi influencia diretamente no .
Para tração (que ocorre na parte inferior da barra) vamos ter:
Já para a compressão (que ocorre na parte superior da barra) vamos ter:
Passo 5
Agora vamos atacar a parte referente ao carregamento:
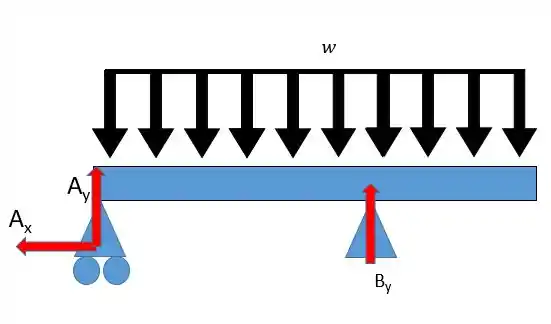
Calculando as forças resultantes, e observando que, como não há forças horizontais então :
Agora o somatório do momento:
Assim,
Não tem problema ficar em função de é assim mesmo!
Passo 6
Agora vamos ter que achar de fato o momento fletor máximo. Para isso a gente tem que achar o ponto onde a força cortante é igual a zero, vamos fazer isso!
Igualando a zero:
Percebe-se, portanto, que
Calculando o momento fletor para essa posição:
Passo 7
Agora vamos achar o momento resistente mínimo que a viga deve possuir , que é dado por:
Novamente vamos ter que fazer em duas etapas, uma para tração e outra para a compressão. Começando pela tração:
Como o carregamento normalmente é dado em podemos multiplicar o numerador por
Para a compressão:
Passo 8
Agora é só comparar esses módulos resistentes. Primeiro para a tração:
Igualando os dois termos:
Para a compressão:
Igualando os dois termos:
Como temos de obdecer aos dois critérios ao mesmo tempo vamos ter que escolher o menor carregamento, desta forma: