Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 5
A força de deve ser decomposta em componentes ao longo das linha e . (a) Usando trigonometria, determine o ângulo sabendo que o componente ao longo de é , (b) Qual é o valor correspondente do componente ao longo de ?
Passo 1
Bom galera, se a gente pensar um pouquinho e brincar com as nossas componentes a gente vai conseguir isso aqui:
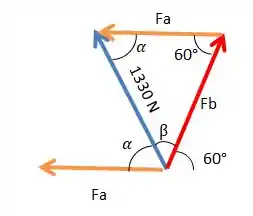
Passo 2
Então, a gente usa a lei dos senos rapidinho assim:
Fazendo aquele famoso esquema do “cruz credo”, a gente fica com:
Usando a função inversa do seno:
Como a soma dos angulos internos de um triângulo é 180°, então:
Passo 3
Belezinha, então vamos usar a lei dos senos denovo pra gente encontrar o componente na linha :
A gente faz denovo o “cruz credo”:
Resposta
Exercícios de Livros Relacionados
Se θ = 30 ° e T = 6 k N , determine a intensidade da força resultante que atua sobre a argola e sua direção, medida no sentido horário a partir do eixo x positivo.
Determine o ângulo de θ para conectar o membro A à chapa de modo que a força resultante de F A e F B seja direcionada horizontalmente para a direita. Além disso, informe qual é a intensidade da força
2.3. Se a intensidade da força resultante deve ser 9 k N direcionada ao longo do eixo x positivo, determine a intensidade da força T que atua sobre a argola e seu ângulo θ.
2.6. Decomponha F 2 em componentes ao longo dos eixos u e v , e determine suas intensidades.
2.1. Se θ = 6 0 ° e T = 5 k N , determine a intensidade da força resultante que atua sobre a argola e sua direção, medida no sentido horário a partir do eixo x positivo.