Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 9
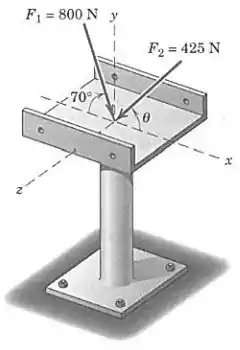
Duas forças são aplicadas ao suporte de construção, como mostrado. Determine o ângulo que faz com que a resultante das duas forças seja vertical. Determine o módulo da resultante.
Passo 1
Primeiro, somamos todas as componentes de força em e igualamos a zero, pois a resultante só deve ter componente vertical:
Passo 2
Como só tem componente vertical, o módulo será:
Resposta
Exercícios de Livros Relacionados
Determine a resultante R das duas forças mostradas(a) aplicando a regra do paralelogramo para a adição vetorial e(b) somando as componentes escalares.
Uma força F de módulo 800N é aplicada ao ponto C da barra A B , como mostrado. Determine os componentes x - y e n - t de F .
O componente t da força F vale 75N . Determine o componente n e o módulo de F .
As duas forças mostradas atuam no ponto A da barra dobrada. Determine a resultante R das duas forças.
Para satisfazer limitações de projeto é necessário determinar o efeito da força trativa de 2k N atuando no cabo, sobre o cisalhamento, a tração e a flexão da viga em I engastada. Com este propósito, s