Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 23
Determine a resultante das duas forças mostradas
(a) aplicando a regra do paralelogramo para a adição vetorial e
(b) somando as componentes escalares.
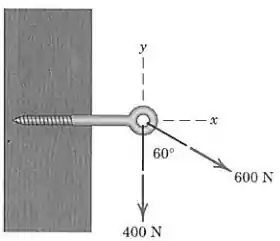
Passo 1
(a) Na figura a seguir, representamos os vetores das forças de e , construindo a resultante a partir da regra do paralelogramo:
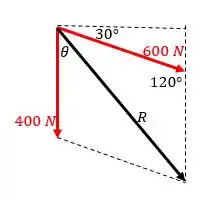
Desse modo, podemos usar a lei dos cossenos para determinar o módulo :
Agora utilizamos a lei dos senos para determinar o ângulo :
Passo 2
(b) Beleza! Agora vamos determinar calculando as componentes e , ao realizar o somatório das componentes em e de todas as forças:
Logo,
Resposta
(a)
(b)
Exercícios de Livros Relacionados
2.37. Se a intensidade da força resultante que atua sobre a chapa precisa ser 6k N e sua direção no sentido horário do eixo x positivo é θ = 30 ° , determine a intensidade de F 2 e o ângulo Φ
2.38. Se Φ = 30 ° e a força resultante que atua sobre a placa de ligação é direcionada ao longo do eixo x positivo, determine as intensidades de F 2 e da força resultante.
135. Determine as componentes x e y da força de 700N
2.44. Se a intensidade da força resultante que atua sobre o suporte é 2k N direcionada ao longo do eixo x positivo, determine a intensidade de F 1 e sua direção Φ
2.50. As três forças são aplicadas no suporte. Determine a faixa de valores para a intensidade da força P, de modo que a resultante das três forças não exceda 2400N .