Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 185

Para a viga curva e o carregamento indicados na figura, determine a tensão no (a) ponto A e (b) ponto B.

Passo 1

Tá legal! A primeira coisa que devemos fazer nesse exercício é separar o trapézio em dois triângulos, para poder encontrar o raio médio da seção, que será dado por:

r - = ∑ A i r - i ∑ A

Então, dividindo a seção em duas, teremos:

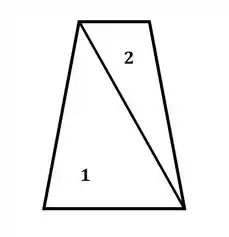
Então, sabendo que a área de um triângulo é dada por:

A = b h 2

Para a área 1, teremos:

A 1 = 0,04 0,03 2 → A 1 = 600 . 10 - 6   m 2

Agora, para a área 2, teremos:

A 2 = 0,0 2 0,03 2 → A 2 = 300 . 10 - 6   m 2

Agora, precisamos encontrar a localização do centroide de cada uma das duas áreas. Sabendo que o centroide de um triângulo está localizado a 1/3 da sua altura (medindo a partir da base), ficou fácil. Para o triângulo 1, teremos:

r - 1 = 35 + 30 3 → r - 1 = 45   m m = 0 , 045   m

Agora, para o triângulo 2, teremos:

r - 2 = 35 + 2 ( 30 ) 3 → r - 2 = 55   m m = 0 , 055   m

Agora conseguimos encontrar o centroide da seção. Então, substituindo os valores conhecidos na primeira equação do passo 1, temos:

r - = ∑ A i r - i ∑ A = 600 . 10 - 6 0 , 045 + 300.10 - 6 0 , 055 600 . 10 - 6 + 300 . 10 - 6

r - = 48,333.10 - 3   m

Passo 2

Agora vamos escrever o raio interno da seção, que pode ser visto através da figura do enunciado como a distância do centroide C até a base do trapézio, então temos:

r 1 = 35   m m = 0 , 035   m

Agora, para o raio externo da seção, que será dado pelo raio interno mais a altura do trapézio, temos:

r 2 = r 1 + h = 35 + 30 → r 2 = 65   m m = 0 , 065   m

Agora, para encontrar a localização do raio da superfície neutra da seção, vamos recorrer a fórmula para a seção trapezoidal apresentada na figura 4.61 dessa seção, dada por:

R = 1 2 h 2 b 1 + b 2 b 1 r 2 - b 2 r 1 ln ⁡ r 2 r 1 - h b 1 - b 2  

Então, substituindo os valores conhecidos, chegamos em:

R = 1 2 0,03 2 0,04 + 0,02 0 , 04 0,065 - 0,02 0 , 035 ln ⁡ 0,065 0 , 035 - 0,03 0,04 - 0,0 2

R = 27 . 10 - 6 1,17617 . 10 - 3 - 0,6 . 10 - 3 → R = 46,861.10 - 3   m

Passo 3

Agora podemos encontrar a excentricidade e da seção, que é a distância entre a linha neutra e o centroide da seção, através de:

e = r - - R

Substituindo os valores conhecidos, teremos:

e = 48,333.10 - 3 - 46,861.10 - 3 → e = 1,4718 . 10 - 3   m

Agora para encontrar a tensão no ponto A pedida na letra (a), vamos utilizar a equação 4.71 vista nessa seção, onde temos:

σ = M r - R A e r

No ponto A temos r = r A = 35   m m , então a equação acima se torna:

σ A = M r A - R A e r A

Substituindo os valores conhecidos, chegamos em:

σ A = - 250 0,035 - 46,861.10 - 3 600.10 - 6 + 300.10 - 6 1,4718.10 - 3 0 , 035

σ A = 63,96   M P a

Passo 4

Agora para encontrar a tensão no ponto B pedida na letra (b), nós vamos repetir o último cálculo do passo 2, só que agora com r = r B = r 2 = 65   m m . Então a equação 4.71 se torna:

σ B = M r B - R A e r B

Substituindo os valores conhecidos, chegamos em:

σ B = - 250 0,06 5 - 46,861.10 - 3 600.10 - 6 + 300.10 - 6 1,4718.10 - 3 0 , 06 5

σ B = - 52,67 M P a

Resposta

a :   σ A = 63,96   M P a

b :   σ B = - 52,67 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga de seção transversal assimétrica está submetida a um momento M 0 atuando no plano vertical x y . Mostre que a tensão no ponto A, de coordenadas y e z , é σ A = - y I y - z I y z I y I z - I y
A barra curva mostrada tem seção transversal de 40 x 60 mm e raio interno r 1 = 15m m . Para o carregamento mostrado, determine as maiores tensões de tração e compressão.
Resolva o Problema 4.167 considerando que β = 60 ° .
As chapas de ligação de aço com a seção transversal mostrada na figura estão disponíveis com diferentes ângulos centrais β . Sabendo que a tensão admissível é de 82,7 MPa, determine a maior força P qu
Para a barra curva e o carregamento mostrado, determine o erro percentual introduzido na computação da tensão máxima admitindo que a barra é reta. Considere o caso em que (a) r 1 = 20m m , (b) r 1 = 2