Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 19
Duas peças de madeira de 80x120mm, de seção transversal retangular e uniforme, são unidas por simples colagem das seções chanfradas, como mostrado. Sabendo-se que as máximas tensões admissíveis na junta são respectivamente de 400KPa na tração(perpendiular ao chanfro) e de 660kPa no cisalhamento(paralelo ao chanfro), determinar a maior carga axial P que pode ser aplicada.
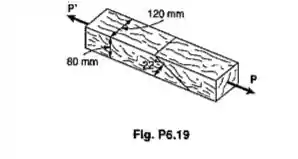
Passo 1
Precisamos primeiro saber a área que a tensão vai atuar. Vamos desenhar e observar.
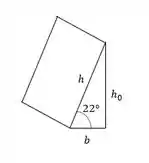
A força vai atuar no plano oblíquo e precisamos da altura h, que é calculada dessa forma.
Passo 2
A força normal precisa ser perpendicular ao plano, então a gente vai decompor ela:
E a tensão normal de tração é:
Resolvendo, temos P:
Passo 3
Precisamos avaliar pela tensão cisalhante, a ideia é parecida, precisamos decompor a força na outra direção.
A área de atuação é a mesma, então:
Considerando :
Temos P:
*Observação: O valor do gabarito é encontrado quando temos , porém o enunciado considera 660KPa, portanto há diferença no valor de P.