A força de é vertical, a força é horizontal, e ambas as forças atuam em planos perpendiculares ao eixo maciço . Sabendo-se que , determinar o menor diâmetro permissível para o eixo .
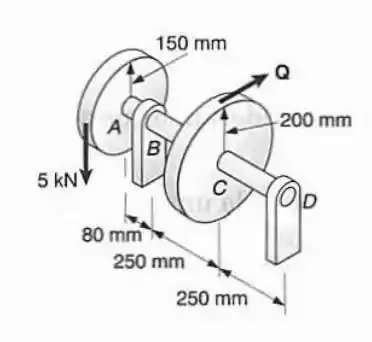
Passo 1
Fala aí, galera! Essa questão faz um pedido bem simples, achar o diâmetro do nosso eixo! Para fazer isso vamos ter que utilizar a seguinte equação:
Onde é o momento polar de inércia é o raio, o momento fletor e a torção, além disso temos também a máxima tensão de cisalhamento admissível .
Então a gente tem que calcular basicamente a torção e o momento fletor no eixo, para calcular isso vamos ter que primeiro achar as reações nos pontos e então vamos lá!
Passo 2
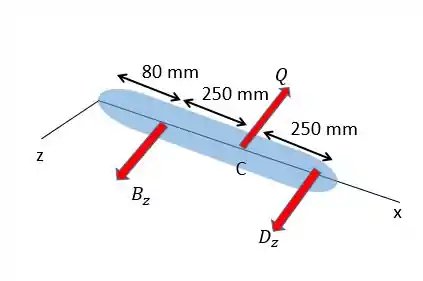
Para começar o problema a gente vai ter que calcular as reações nos pontos e conforme o desenho abaixo vamos fazer isso começando pelas relações de forças:
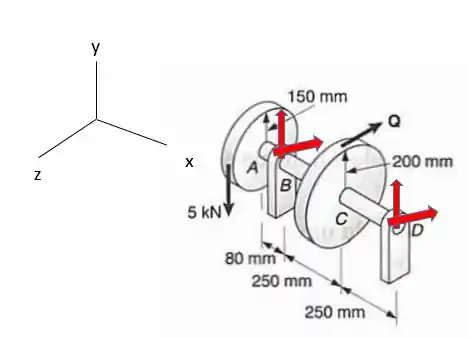
utilizando as equações da estática vamos ter:
Resolvendo:
Para as forças em :
Passo 3
Agora vamos partir para os momentos.
Para o momento em em relação ao ponto :
Logo
Substituindo na equação:
vamos ter:
Agora o momento em em relação ao ponto :
Podemos substituir na equação:
E obter:
Agora o momento em novamente em relação ao ponto :
Então nós achamos todos os valores que queríamos:
Podemos ainda substituir em e :
Passo 4
Neste passo vamos calcular o torque de cada seção, para isso vamos dividir em duas partes e . Vamos começar pela parte :
Lembrando que o torque é calculado como:
De até existe apenas um torque, o da força de então vamos ficar com:
E vamos calcular o torque em , aqui o torque da força de anula o torque da força assim:
Show de bola!
Passo 5
Agora temos de calcular também os momentos fletores de cada seção. Para fazer isso fica mais fácil se fizermos um diagrama com os dados que achamos no passo 3:
obs: Aqui os sinais negativos foram retirados porque já foram compensados nos sentidos das forças.
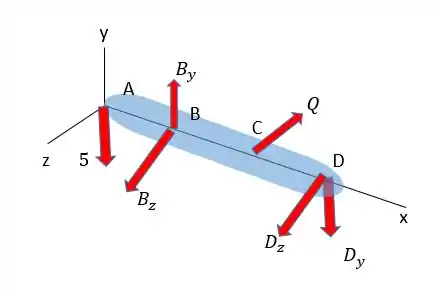
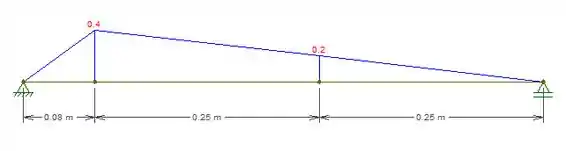
Mas para ficar mais fácil vamos dividir em duas figuras, uma mostrando apenas as forças em e outra apenas as força em . Vamos começar pelas forças em :
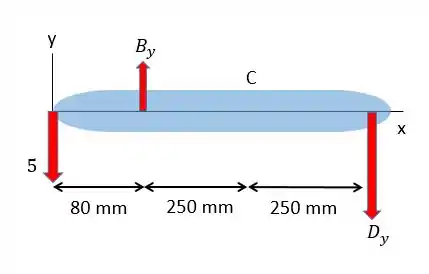
Com isso vamos poder calcular os momentos que serão iguais a:
Colocando num gráfico vamos ter:
Agora vamos olhar para os momentos em :
No gráfico vamos ter:
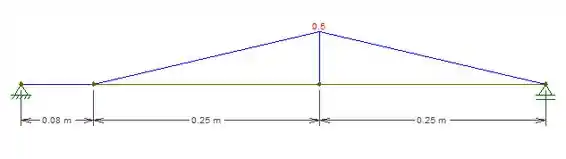
Beleza, agora temos todos os momentos e torques atuantes na barra!
Passo 6
Agora vamos aplicar a relação entre torque e tensão cisalhante que é dada por:
No nosso caso como temos momento em mais de um eixo vamos ter:
Agora vamos ter que pegar a seção do eixo que irá fornecer o maior valor de:
Então vamos ter que utilizar o ponto . Obtendo:
Passo 7
Precisamos calcular o valor do momento polar de inércia:
Então vamos ter:
Substituindo na equação: