Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 151
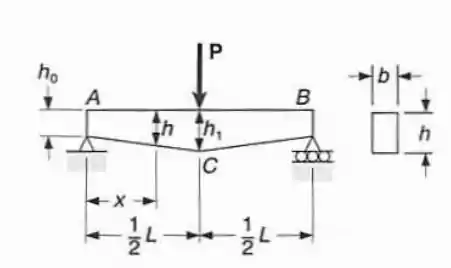
Para a viga com o carregamento mostrado, determinar: (a) a seção transversal onde ocorre a máxima tensão normal; (b) a correspondente tensão normal máxima. Assumir
Passo 1
Fala aí, pessoal!!!
Neste problema a gente tem que reparar que a seção transversal muda conforme avançamos na viga. É importante perceber que a seção é sempre um retângulo o que muda é a altura.
Então vai ser importante representar corretamente essa variação de altura em função de para calcularmos o módulo resistente da seção e finalmente aplicarmos a equação:
Passo 2
Vamos começar calculando o módulo resistente dessa seção, lembrando que o módulo resistente é calculado como:
Como temos um retângulo, vamos ter:
E
Assim vamos ficar com:
Passo 3
Beleza, mas esse não varia? Então vamos expressar essa variação.
A gente pode ver pelo desenho que é uma variação linear então podemos expressar aplicando uma semelhança de triângulos:
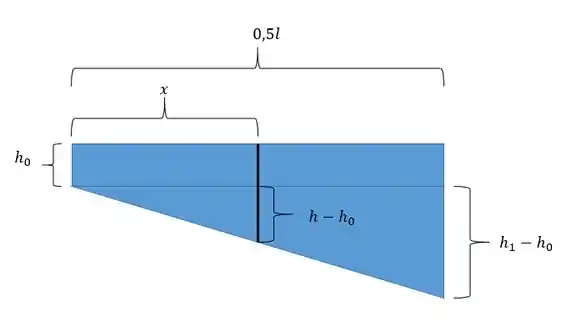
Então podemos expressar o nosso módulo resistente como:
Passo 4
Agora vamos calcular o momento fletor que atua nessa viga, olha só o esquema das forças:
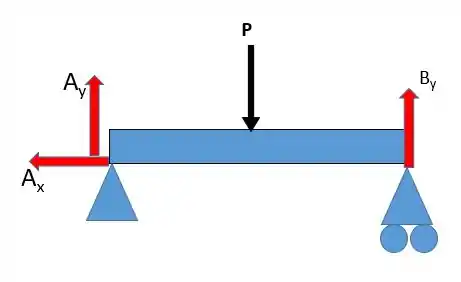
Podemos perceber que já que é a única força que atua na horizontal. Agora vamos fazer o somatório das forças em :
Mas repare que o carregamento é simétrico, então os termos e são iguais!
Agora podemos calcular o momento fletor da barra que é igual a:
obs: Aqui a gente calcuou só para a metade da esquerda da barra, mas como ela é simétrica então não precisamos calcular tudo, só metade mesmo =D
Passo 5
Se a gente já tem o módulo resistente e o momento fletor vamos aplicar a equação da tensão:
Simplificando:
Agora, para achar o máximo dessa equação vamos derivar e igualar a zero e para ficar mais simples vamos considerar:
Então vamos ter:
Derivando:
Como o numerador deve ser igual a zero:
Como
Então
Passo 6
Agora é só aplicar a equação da tensão máxima para esse ponto!
Para facilitar vamos substituir o valor de separado:
E
Substituindo:
Resposta
a)
b)