Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 9.Problemas de Revisão - Ex. 112a
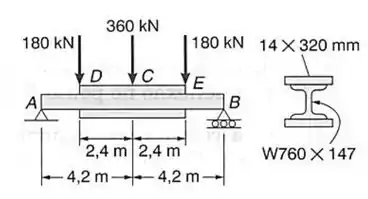
Duas placas de cobertura são soldadas a uma viga de perfil laminado de aço , como mostrado. Usando , determinar:
- A declividade na extremidade A
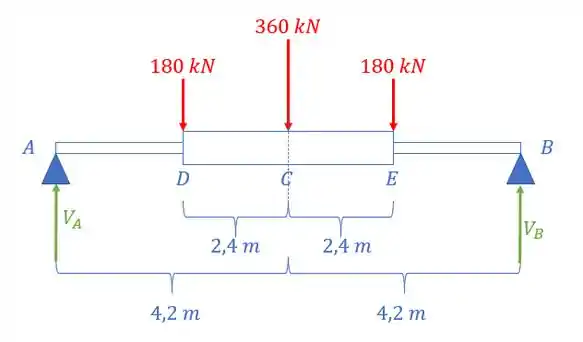
Passo 1
Fala galera, antes de tudo para o nosso problema, podemos determinar as reações de apoio, mas depois, poderemos jogar metade da nossa viga fora. Por ela ser simétrica, poderemos fazer todas as nossas contas com base na primeira metade dela, partiu?
Agora vamos fazer uma pequena mudança, ao invés de irmos para o diagrama, vamos determinar os momentos de inércia:
- Momento de inércia da viga sozinha
- Momento de inércia da viga com as barras
Desse modo, podemos dizer que as rigidezes serão dadas por:
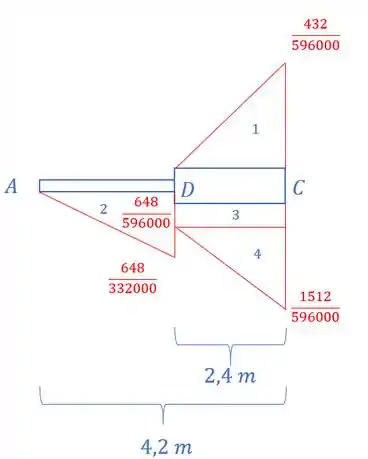
Assim podemos desenhar os nossos diagramas, nesse caso faremos o seguinte, vamos considerar que tiramos o apoio em A e a reação dele consideramos como uma carga na viga. E para isso, vamos considerar que em C temos um engaste, ou seja, podemos desenhar o diagrama de cada viga até o ponto C, assim, teremos que:
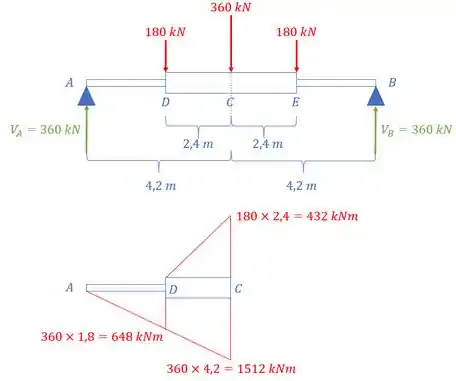
Dividindo o valor para o EI correspondente, tem-se que:
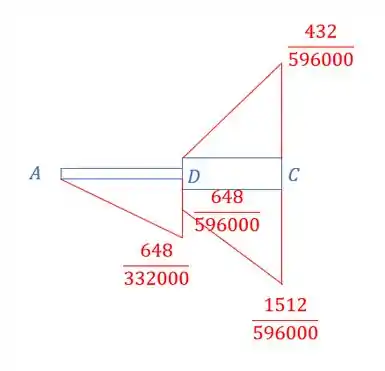
Passo 2
Podemos calcular o ângulo em C com relação a A do seguinte modo:
Sabemos pela simetria que o ângulo em C é zero, desse modo, teremos que:
E para determinação de precisamos da área entre A e C, assim, teremos que:
