Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 144
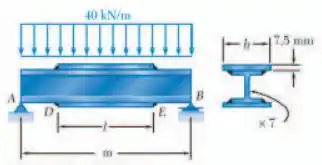
Duas placas de reforço com de espessura, são soldadas a uma viga , conforme mostra a figura. Sabendo que e , determine a tensão normal máxima em uma seção na transversal no centro da viga e imediatamente à esquerda de .
Passo 1
Fala aí, pessoal. Beleza? Bora zerar esse livro.
Este problema nos pede para determinarmos a tensão normal máxima no centro da viga e também, em uma seção imediatamente à esquerda de . Primeiro, vamos esboçar o DCL:
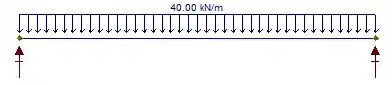
Sabendo disso, vamos calcular a reação de apoio através das equações de equilíbrio:
Por simetria, temos que , logo:
Com isso, podemos determinar a equação para o momento fletor pela equação de equilíbrio para o segmento . Temos:
Agora a gente já pode determinar os momentos no ponto e no ponto . Para isso, basta substituirmos na equação que a gente encontrou. Para o primeiro, temos:
E para o ponto :
Passo 2
Em seguida, já que temos os momentos nos pontos em que devemos calcular a máximatensão, precisamos encontrar as outras variáveis da qual ela depende. Sabemos que a tensão normal causada pelo momento fletor é dada por:
Onde é a distância para a linha neutra e é o momento de inércia. Podemos achar o valor de pela seguinte relação:
Para calcularmos o momento de inércia, temos uma viga de perfil e duas placas de reforço. Assim, o momento de inercia vai ser o somatório do momento de inércia deles. Fica assim:
O momento de inércia para o perfil é encontrado no ábaco e é dado por:
Então, substituindo:
Passo 3
Por fim, basta substituirmos o momento fletor respectivo para cada caso na fórmula da tensão que a gente comentou acima. A tensão normal máxima no centro da viga vai ser dada por:
E para a tensão no ponto imediatamente após o ponto , temos:
É isso, galera! Bora fazer mais exercícios pra ficar craque.