Duas rodas em formato de disco, cada uma com massa , estão ligadas por uma barra leve, porém rígida de comrpimento . O conjunto é arremessado de uma superfície horizontal, com velocidade conforme indicado. Se é suficientemente grande para que a barra não toque na quina após ter deixado a superfície, determine um valor aproximado para a velocidade angular do conjunto, uma vez que tenha ultrapassado a superfície. Considere as rodas como massas concentradas, e mencione quaisquer outras hipóteses simplificadoras.

Passo 1
O que vai provocar a rotação da barra conforme a roda se aproxima da borda? O momento gerado pelo peso do conjunto!
O enunciado diz que a velocidade é grande o suficiente para que a barra não toque a quina depois que passa da borda.
Mas vamos assumir também que é grande o suficiente para que o ângulo que a barra forma com a horizontal depois que passa a borda é pequeno, de forma que podemos fazer a seguinte aproximação:
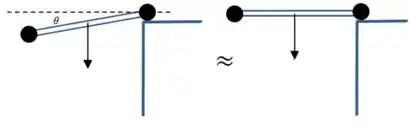
Passo 2
Agora que fizemos essa aproximação, vamos fazer um diagrama de forças:
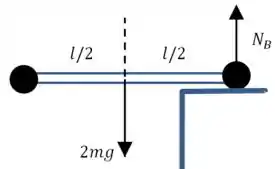
Esse diagram vale para qualquer instante de tempo desde quando passa a borda, até quando chega na borda. E podemos escrever uma equação de momentos em relação ao ponto :
Olhando primeiro para o lado direito da equação, a única força que produz momento em relação ao ponto é a força peso:
E o momento de inércia em relação ao ponto pode ser encontrado usando o teorema dos eixos paralelos:
Então:
Passo 3
Agora que conhecemos a aceleração angular, como podemos encontrar a velocidade angular no instante em que atinge a borda?
E se a velocidade da roda é constante, o tempo que ela demora para atingir a borda depois que já a atingiu é:
E , então:
Resposta
A velocidade angular do conjunto será .