Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 61
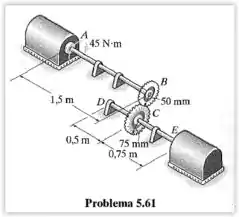
Os eixos de de diâmetro são feitos de aço-ferramenta L2 e estão apoiados em mancais que permitem aos eixos girarem livremente. Se o motor em desenvolver um torque no eixo , enquanto a turbina em é fixa e não pode girar, determine a quantidade de rotação das engrenagens e .
Passo 1
Olá, galera! E aí, vamos responder essa questão?
O enunciado nos fornece os seguintes dados:
Aço-ferramenta L2, portanto,
Começaremos fazendo uma análise da figura: quando o motor desenvolve em o torque no sentido horário, ele faz com que a engrenagem gire no mesmo sentido. Esse movimento vai fazer com que a engrenagem gire no sentido anti-horário.
Calculando o torque no eixo , temos que:
Em que R é o raio da engrenagem. Então:
Igualando as forças, temos:
Passo 2
Encontraremos primeiro o ângulo :
O momento polar de inércia, , é dado por:
Simplicando e substituindo, temos:
Convertendo para graus:
Passo 3
E agora determinaremos o ângulo :
Convertendo para graus: