Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 62

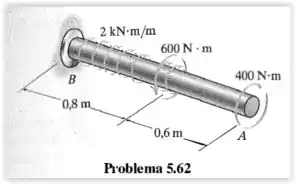
O eixo maciço de de diâmetro é feito de aço A-36 e está sujeito aos carregamentos de torção distribuídos e concentrados mostrados na figura. Determine o ângulo de torção na extremidade livre do eixo devido a esses carregamentos.

Passo 1

Olá, pessoal! Tudo bem?

O enunciado nos fornece os seguintes dados:

Aço A-36, portanto,

E pede que determinemos o ângulo de torção na extremidade livre . Podemos observar pela imagem, que há uma distrubuição de torque do ponto (fixo), até uma distância no eixo, onde vamos nomear de ponto .

A ideia é que o ângulo em vai ser a soma do ângulo das seções e .

Precisamos dos torques em cada seção. Vamos então construir o diagrama de corpo livre das seções e :

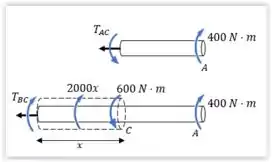
Aí a gente acha esses carinhas!

Passo 2

O torque interno no seguimento é constante. (está entre dois torques pontuais) Pelo diagrama de corpo livre, temos:

Passo 3

Observe o diagrama de corpo livre. Para obtermos o torque distribuído ao longo do segmento , fazemos um corte, há uma distância do ponto e multiplicamos o valor do carregamento de torção por essa distância:

Fazendo o somatório dos momentos em todo o eixo AB, temos:

Prontinho, achamos os torques nas duas seções.

Passo 4

O ângulo é determinado pelo ângulo causado por . Observando sempre o sentido dos torques. Como no nosso DCL eles tem sentidos opostos, fazemos:

Repara que para o torque em que é constante, usamos a fórmula comum para o ângulo. Mas para que é uma função de , precisamos usar a carinha de integral do ângulo. Basicamente, a gente em vez de multiplicar por , nós integramos de a .