Quando um poço é perfurado, considera-se que a extremidade do tubo da perfuratriz que se aprofunda no solo encontra uma resistência à torção T A . Além disso, o atrito do solo ao longo das laterais do tubo cria uma distribuição linear de torque por unidade de comprimento que varia de zero na superfície B a t 0 em A . Determine o torque necessário T B que deve ser fornecido pela unidade de acionamento para girar o tubo. Calcule também o ângulo de torção relativo de uma extremidade do tubo em relação à outra extremidade no instante em que o tubo está prestes a girar. O tubo tem raio externor o e raio interno r i . O módulo de cisalhamento é G .

ϕ B / A = 2 ⋅ L( 3 T A + t 0 ⋅ L ) 3 ⋅ π r 0 4 - r i 4 ⋅ G

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 63

Quando um poço é perfurado, considera-se que a extremidade do tubo da perfuratriz que se aprofunda no solo encontra uma resistência à torção . Além disso, o atrito do solo ao longo das laterais do tubo cria uma distribuição linear de torque por unidade de comprimento que varia de zero na superfície a em . Determine o torque necessário que deve ser fornecido pela unidade de acionamento para girar o tubo. Calcule também o ângulo de torção relativo de uma extremidade do tubo em relação à outra extremidade no instante em que o tubo está prestes a girar. O tubo tem raio externo e raio interno . O módulo de cisalhamento é .

Passo 1

A questão quer que determinemos a torção em e o ângulo de torção relativo de uma extremidade do tubo em relação à outra extremidade no instante em que o tubo está prestes a girar, ou seja, quando os torques estiverem em equilíbrio. Para isso nos fornece:

Começaremos logo calculando o momento polar de inércia:

Vamos agora calcular o torque em , pois é com ele que iremos encontrar a deformação . Para isso temos que realizar um somatório dos torques. Vamos analisar a figura para melhor entender o problema.

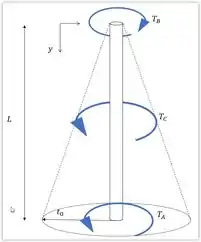
O torque gerado pelo carregamento é o torque resultante da distribuição linear de torque que varia entre . O torque total gerado por esse carregamento é a área de um triângulo de base e altura . Resultando em:

Com isso nosso somatório é:

Passo 2

Com o torque em encontrado, agora devemos achar o torque total . Analisaremos a imagem para melhor compreensão.

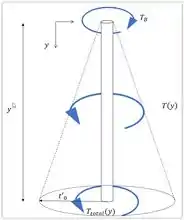
Como podemos notar, torque total que age em sofre influência de e de um torque que varia com o comprimento causado pelo carregamento . Para achar esse segundo torque iremos fazer uma relação de triângulos.

Logo o nosso será:

Sendo assim o nosso somatório de torques resulta em um igual a;

Passo 3

Agora só falta encontrar o ângulo de torção do eixo;

Como previamente foi calculado o valor de , substituindo temos como resultado:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um torque de 1,2 kNm é aplicado a uma barra vazada de alumínio que tem a seção mostrada na figura. Desprezando-se o efeito da concentração de tensões, determinar a tensão de cisalhamento na barra

Sabendo-se que a varra do Prop 3.127 tem 900 mm de comprimento e que G = 26G P a , determinar o ângulo de torção causado pelo torque 1,2 kNm

Um eixo cilíndrico vazado foi projetado com a seção transversal mostrada na Fig (1) para resistir a um torque máximo T 0 . Um defeito na fabricação, no entanto, resultou em uma pequena excentricidade

As especificações de projeto de um eixo de transmissão de seção cheia de 1,2 m de comprimento requerem que o ângulo de torção do eixo não exceda 4° quando for aplicado um torque de 750N / m . Determin

A haste cilíndrica cheia BC de comprimento L = 24i n . é conectada na alavanca rígida AB de comprimento a = 15i n , e no suporte C. Especificações de projeto exigem que o deslocamento de A não exceda