Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 59

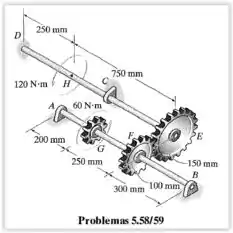
Os dois eixos são feitos de aço A-36. Cada um tem diâmetro de e ambos estão apoiados em mancais em , e que permitem livre rotação. Se o apoio em for fixo, determine o ângulo de torção da extremidade quando os torques são aplicados ao conjunto como mostra a figura.

Passo 1

Olá, pessoal! Tudo bem?

O enunciado nos fornece os seguintes dados:

Aço A-36, portanto,

Começaremos fazendo uma análise da figura: o eixo está apoiado por um mancal em . Se a engrenagem gira no sentido anti-horário, consequentemente a engrenagem também, e podemos observar que , afinal os apoios no eixo permitem que ele rotacione e , portanto, não geram torque de reação e além disso não há outros torques nesse eixo.

Como resultado do movimento de no sentindo anti-horário, a engrenagem vai girar no sentido horário, portanto oposto ao torque .

Queremos descobrir o ângulo de torção em . Como em temos um engaste, o ângulo ali é zero. Então para determinar o ângulo absoluto, vamos analisar os ângulos de até . Aí nosso ângulo em vai ser a soma dos ângulos das seções (que depende do eixo de ) e .

Vamos achar esses carinhas!

Passo 2

Vamos achar o torque no eixo , temos que para um torque qualquer

Em que R é o raio da engrenagem e a força que gera o torque.

Sabendo que a força atuando nas engrenagens é a mesma e fazendo uma relação entre as engrenagens e , sabendo que é o raio da engrenagem em e da engrenagem em , temos:

Fazendo o somatório dos momentos torsores, descobrimos o valor do torque :

Passo 3

Vamos agora calcular o ângulo de torção em . E para isso, vamos achar o ângulo em .

Já descobrimos os torques, seus sentidos de ação e a forma como conjunto vai funcionar.

Portanto, podemos notar que vai ser determinado pelo ângulo de torção no eixo menos o ângulo de torção no eixo (ângulos em sentidos opostos, porque tem torques de sentidos opostos).